【题目】如图,矩形OABC的边OA在x轴上,O与原点重合,OA=1,OC=2,点D的坐标为(2,0),则直线BD的函数表达式为( ).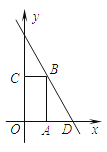
A.y=-x+2
B.y=-2x+4
C.y=-x+3
D.y=2x+4
参考答案:
【答案】B
【解析】因为OA=1,OC=2,
所以BC=1,AB=2,
所以点B的坐标是(1,2),
又∵点D的坐标是(2,0),
设直线CBD的关系式为y=kx+b ,
把B , D的坐标代入关系式,有 ![]() 解得
解得 ![]() ∴直线CD的函数关系式是y=-2x+4
∴直线CD的函数关系式是y=-2x+4
选:B.
【考点精析】根据题目的已知条件,利用确定一次函数的表达式的相关知识可以得到问题的答案,需要掌握确定一个一次函数,需要确定一次函数定义式y=kx+b(k不等于0)中的常数k和b.解这类问题的一般方法是待定系数法.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,过A点的一次函数的图象与正比例函数y=2x的图象相交于点B , 则这个一次函数的解析式是( ).

A.y=2x+3
B.y=x-3
C.y=2x-3
D.y=-x+3 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将周长为8的△ABC沿BC方向向右平移1个单位得到△DEF,则四边形ABFD的周长为

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,是二次函数y=ax2+bx+c图象的一部分,图象过点A(﹣3,0),对称轴为直线x=﹣1,给出四个结论:
①b2>4ac ②2a+b=0 ③c﹣a<0 ④若点B(﹣4,y1)、C(1,y2)为函数图象上的两点,则y1<y2,其中正确结论是( )

A.②④ B.②③ C.①③ D.①④
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD的边长为10,AG=CH=8,BG=DH=6,连接GH,则线段GH的长为( )
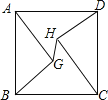
A.
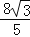 B.2
B.2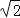 C.
C.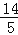 D.10﹣5
D.10﹣5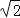
-
科目: 来源: 题型:
查看答案和解析>>【题目】下表是某小区15户居民今年3月份的用水情况统计表:
月用水量(吨/户)
5
8
12
15
18
居民(户数)
1
2
3
4
5
则今年3月这15户居民用水量的中位数是( )
A.8B.12C.15D.18
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一次函数y=kx+b(k≠0)图象过点(0,2),且与两坐标轴围成的三角形面积为2,则一次函数的解析式为( ).
A.y=x+2
B.y=-x+2
C.y=x+2或y=-x+2
D.y=-x+2或y=x-2
相关试题

