【题目】如图①,在矩形 ABCD中,AB=10cm,BC=8cm.点P从A出发,沿A→B→C→D路线运动,到D停止;点Q从D出发,沿 D→C→B→A路线运动,到A停止.若点P、点Q同时出发,点P的速度为每秒1cm,点Q的速度为每秒2cm,a秒时点P、点Q同时改变速度,点P的速度变为每秒bcm,点Q的速度变为每秒dcm.图②是点P出发x秒后△APD的面积S1(cm2)与x(秒)的函数关系图象;图③是点Q出发x秒后△AQD的面积S2(cm2)与x(秒)的函数关系图象.
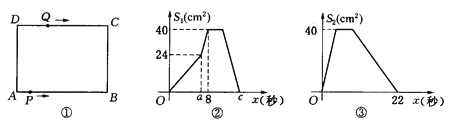
(1)、参照图象,求b、图②中c及d的值;
(2)、连接PQ,当PQ平分矩形ABCD的面积时,运动时间x的值为 ;
(3)、当两点改变速度后,设点P、Q在运动线路上相距的路程为y(cm),求y(cm)与运动时间x(秒)之间的函数关系式,并写出自变量x的取值范围;
(4)、若点P、点Q在运动路线上相距的路程为25cm,求x的值.
参考答案:
【答案】(1)、b=2;C=17;d=1;(2)、![]() ;(3)、当6<x≤
;(3)、当6<x≤![]() 时,y=28-3x 当
时,y=28-3x 当![]() <x≤17时,y=3x-28;当17<x≤22时,y=x+6;(4)、1秒或19秒.
<x≤17时,y=3x-28;当17<x≤22时,y=x+6;(4)、1秒或19秒.
【解析】
试题分析:(1)、首先根三角形面积求出a的值,然后得出b、c、d的值;(2)、平分面积则说明PQ经过四边形对角线的交点;(3)、利用待定系数法分别求出两段函数图像的解析式;(4)、分别根据改变速度前和改变速度后两种情况求出x的值.
试题解析:(1)、观察图②得S△APD=![]() PA
PA![]() AD=
AD=![]() ×a×8=24, ∴a=6(秒),
×a×8=24, ∴a=6(秒),
![]() (厘米/秒),
(厘米/秒), ![]() (秒);
(秒);
(22﹣6)d=28﹣12, 解得d=1(厘米/秒);
(2)、![]()
(3)、当6<x≤![]() 时,y=28-3x 当
时,y=28-3x 当![]() <x≤17时,y=3x-28 当17<x≤22时,y=x+6
<x≤17时,y=3x-28 当17<x≤22时,y=x+6
(4)、改变速度前,28-3x=25,x=1
改变速度后,x+6=25,x=19
∴当点Q出发1或19秒时,点P、点Q在运动路线上相距的路程为25cm.
-
科目: 来源: 题型:
查看答案和解析>>【题目】方程3x﹣y=4中,有一组解x与y互为相反数,则3x+y=_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将矩形纸片ABCD沿对角线AC折叠,使点B落到点B′的位置,AB′与CD交于点E.

(1)试找出一个与△AED全等的三角形,并加以证明.
(2)若AB=8,DE=3,P为线段AC上的任意一点,PG⊥AE于G,PH⊥EC于H,试求PG+PH的值,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD是⊙O的内接四边形,BC的延长线与AD的延长线交于点E,且DC=DE.
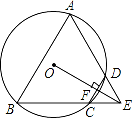
(1)求证:∠A=∠AEB;
(2)连接OE,交CD于点F,OE⊥CD,求证:△ABE是等边三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是2015年12月月历.
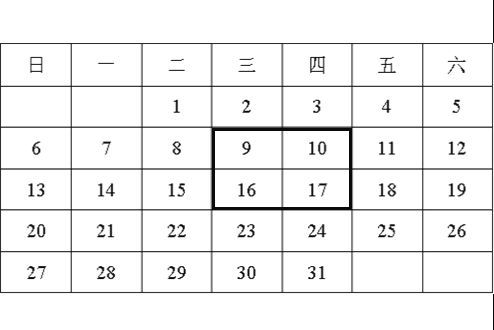
(1)如图,用一正方形框在表中任意框往4个数,记左上角的一个数为x,则另三个数用含x的式子表示出来,从小到大依次是 , , .
(2)在表中框住四个数之和最小记为a1,和最大记为a2,则a1+a2= .
(3)当(1)中被框住的4个数之和等于76时,x的值为多少?
(4)在(1)中能否框住这样的4个数,它们的和等于92?若能,则求出x的值;若不能,则说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】以点A为顶点作两个等腰直角三角形(△ABC,△ADE),如图1所示放置,使得一直角边重合,连接BD,CE.

(1)说明BD=CE;
(2)延长BD,交CE于点F,求∠BFC的度数;
(3)若如图2放置,上面的结论还成立吗?请简单说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在三只乒乓球上,分别写有三个不同的正整数(用a、b、c表示),三只乒乓球除标的数字不同外,其余都相同,将三只乒乓球放在一个不透明的盒中搅拌均匀,无放回的从中依次摸出2只乒乓球,将球上面的数字相加求和.当和为偶数时,记为事件A,当和为奇数时,记为事件B.
(1)设计一组a、b、c的值,使得事件A为必然发生的事件.
(2)设计一组a、b、c的值,使得事件B发生的概率大于事件A发生的概率.
相关试题

