【题目】已知:如图,AB∥CD,E是AB的中点,∠CEA=∠DEB.
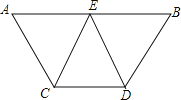
(1)试判断△CED的形状并说明理由;
(2)若AC=5,求BD的长.
参考答案:
【答案】(1)△CED是等腰三角形;(2)5.
【解析】
试题分析:(1)根据平行线的性质得到∠AEC=∠ECD,∠BED=∠EDC,等量代换得到∠ECD=∠EDC,即可得到结论;
(2)由E是AB的中点,得到AE=BE,推出△AEC≌△BED,根据全等三角形的性质即可得到结论.
解:(1)△CED是等腰三角形,
∵AB∥CD,
∴∠AEC=∠ECD,∠BED=∠EDC,
∵∠CEA=∠DEB,
∴∠ECD=∠EDC,
∴△CED是等腰三角形;
(2)∵E是AB的中点,
∴AE=BE,
在△AEC与△BED中,
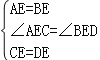 ,
,
∴△AEC≌△BED,
∴BD=AC=5.
-
科目: 来源: 题型:
查看答案和解析>>【题目】经统计我市去年共引进世界500强外资企业19家,累计引进外资410000000美元,数字410000000用科学记数法表示为( )
A.41×107 B.4.1×108 C.4.1×109 D.0.41×109
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列运动属于平移的是( )
A. 荡秋千 B. 地球绕着太阳转 C. 风筝在空中随风飘动 D. 急刹车时,汽车在地面上的滑动
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知反比例函数y=
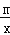 的图象与一次函数y=ax+b的图象相交于点A(1,4)和点B(n,﹣2).
的图象与一次函数y=ax+b的图象相交于点A(1,4)和点B(n,﹣2).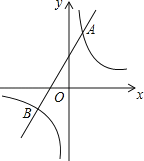
(1)求反比例函数和一次函数的解析式;
(2)当一次函数的值小于反比例函数的值时,直接写出x的取值范围.
-
科目: 来源: 题型:
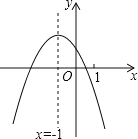
查看答案和解析>>【题目】二次函数y=ax2+bx+c(a≠0)的图象如图,给出下列四个结论:
①4ac﹣b2<0;②4a+c<2b;③3b+2c<0;④m(am+b)+b<a(m≠﹣1),
其中正确结论的个数是( )
A.4个 B.3个 C.2个 D.1个
-
科目: 来源: 题型:
查看答案和解析>>【题目】一种零件的直径尺寸在图纸上是30±0.03(单位:mm),它表示这种零件的标准尺寸是30mm,加工要求尺寸最大不超过( )
A. 0.03 B. 0.02
C. 30.03 D. 29.98
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点O是直线AB上任一点,射线OD和射线OE分别平分∠AOC和∠BOC.
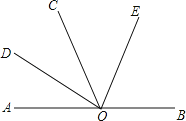
(1)填空:与∠AOE互补的角是 ;
(2)若∠AOD=36°,求∠DOE的度数;
(3)当∠AOD=x°时,请直接写出∠DOE的度数.
相关试题

