【题目】暴雨过后,某地遭遇山体滑坡,武警总队派出一队武警战士前往抢险.半小时后,第二队前去支援,平均速度是第一队的1.5倍,结果两队同时到达.已知抢险队的出发地与灾区的距离为90千米,两队所行路线相同.
(1)问两队的平均速度分别是多少?
参考答案:
【答案】
(1)
解:设第一队的平均速度是x千米/时,
则第二队的平均速度是1.5x千米/时.
根据题意,得: ![]()
解这个方程,得
x=60
经检验,x=60是所列方程的根,
1.5x=1.5×60=90(千米/时).
答:第一队的平均速度是60千米/时,第二队的平均速度是90千米/时
;
解:设第一队的平均速度是x千米/时,
则第二队的平均速度是1.5x千米/时.
根据题意,得: ![]()
解这个方程,得
x=60
经检验,x=60是所列方程的根,
1.5x=1.5×60=90(千米/时).
答:第一队的平均速度是60千米/时,第二队的平均速度是90千米/时
;解:设第一队的平均速度是x千米/时,
则第二队的平均速度是1.5x千米/时.
根据题意,得: ![]()
解这个方程,得
x=60
经检验,x=60是所列方程的根,
1.5x=1.5×60=90(千米/时).
答:第一队的平均速度是60千米/时,第二队的平均速度是90千米/时
【解析】设第一队的平均速度是x千米/时,则第二队的平均速度是1.5x千米/时.根据半小时后,第二队前去支援,结果两队同时到达,即第一队与第二队所用时间的差是 ![]() 小时,即可列方程求解.
小时,即可列方程求解.
【考点精析】本题主要考查了分式方程的应用的相关知识点,需要掌握列分式方程解应用题的步骤:审题、设未知数、找相等关系列方程、解方程并验根、写出答案(要有单位)才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】动点A从原点出发向数轴负方向运动,同时,动点B也从原点出发向数轴正方向运动,运动到3秒钟时,两点相距15个单位长度.已知动点A、B的运动速度比之是3:2(速度单位:1个单位长度/秒).
(1)求两个动点运动的速度;
(2)A、B两点运动到3秒时停止运动,请在数轴上标出此时A、B两点的位置;
(3)若A、B两点分别从(2)中标出的位置再次同时开始在数轴上运动,运动的速度不变,运动的方向不限,问:经过几秒钟,A、B两点之间相距4个单位长度?
-
科目: 来源: 题型:
查看答案和解析>>【题目】在数
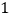 、
、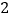 、
、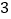 、
、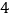 、…、
、…、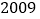 、
、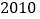 的每个数字前添上“+”或“-”,使得算出的结果是一个最小的非负数,请写出符合条件的式子:________.
的每个数字前添上“+”或“-”,使得算出的结果是一个最小的非负数,请写出符合条件的式子:________. -
科目: 来源: 题型:
查看答案和解析>>【题目】问题情境:一粒米微不足道,平时在饭桌上总会毫不经意地掉下几粒,甚至有些挑食的同学把整碗米饭倒掉.针对这种浪费粮食现象,老师组织同学们进行了实际测算,称得
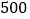 粒大米约重
粒大米约重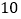 克.
克.尝试解决:
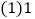 粒米重约多少克?
粒米重约多少克?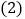 按我国现有人口
按我国现有人口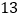 亿,每年
亿,每年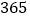 天,每人每天三餐计算,若每人每餐节约
天,每人每天三餐计算,若每人每餐节约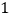 粒大米,一年大约能节约大米多少千克?(结果用科学记数法表示)
粒大米,一年大约能节约大米多少千克?(结果用科学记数法表示)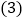 假设我们把一年节约的大米卖成钱,按每千克
假设我们把一年节约的大米卖成钱,按每千克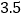 元计算,可卖得人民币多少元?(结果用科学记数法表示,保留到
元计算,可卖得人民币多少元?(结果用科学记数法表示,保留到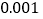 )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示的正方形网格中,△ABC的顶点均在格点上,请在所给直角坐标系中按要求画图和解答下列问题:
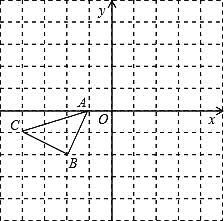
(1)以A点为旋转中心,将△ABC绕点A顺时针旋转90°得△AB1C1,画出△AB1C1.
(2)作出△ABC关于坐标原点O成中心对称的△A2B2C2.
(3)作出点C关于x轴的对称点P.若点P向右平移x(x取整数)个单位长度后落在△A2B2C2的内部,请直接写出x的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在□ABCD中,∠BAD的平分线交BC于点E,∠ABC的平分线交AD于点F,AE与BF相交于点O,连接EF

(1)求证:四边形ABEF是菱形;
(2)若AE=6,BF=8,CE=
 ,求□ABCD的面积.
,求□ABCD的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,把矩形COAB绕点C顺时针旋转α角,得到矩形CFED.设FC与AB交于点H,且A(0,3),C(5,0).
(1)当α=60°时,△CBD的形状是 _________ ;
(2)当0°<α<90°旋转过程中,连结OH,当△OHC为等腰三角形时,请直接写出点H的坐标.

相关试题

