【题目】已知:如图,在直角梯形ABCD中,AD∥BC,∠C=90°,BC=CD,点E、F分别在边BC、CD上,且BE=DF=AD,联结DE,联结AF、BF分别与DE交于点G、P. 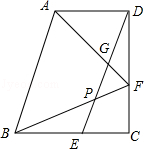
(1)求证:AB=BF;
(2)如果BE=2EC,求证:DG=GE.
参考答案:
【答案】
(1)证明:∵BC=CD,BE=DF,
∴CF=CE,
在△BCF与△DCE中,
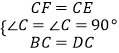 ,
,
∴△BCF≌△DCE,
∴BF=DE,
∵AD∥BC,BE=AD,
∴四边形ABED是平行四边形;
∴AB=DE,
∴AB=BF
(2)证明:延长AF交BC延长线于点M,则CM=CF;
∵AD∥BC,
∴ ![]() =
= ![]() ,
,
∵BE=2EC,
∴ ![]() =
= ![]() =1,
=1,
∴DG=GE.
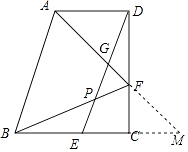
【解析】(1)先证△BCF≌△DCE,再证四边形ABED是平行四边形,从而得AB=DE=BF.(2)延长AF交BC延长线于点M,从而CM=CF,又由AD∥BC可以得到 ![]() =
= ![]() =1,从而DG=GE.
=1,从而DG=GE.
【考点精析】认真审题,首先需要了解直角梯形(一腰垂直于底的梯形是直角梯形),还要掌握相似三角形的判定与性质(相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方)的相关知识才是答题的关键.
-
科目: 来源: 题型:
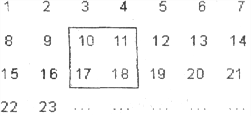
查看答案和解析>>【题目】把正整数1,2,3,4,……,2009排列成如图所示的一个表
(1)用一正方形在表中随意框住4个数,把其中最小的数记为x,另三个数用含x的式子表示出来,从小到大依次是 , , 。
(2)当被框住的4个数之和等于416时,x的值是多少?
(3)被框住的4个数之和能否等于622?如果能,请求出此时x的值;如果不能,请说明理由。
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:点A在射线CE上,∠C=∠D.
(1)如图1,若AC∥BD,求证:AD∥BC;
(2)如图2,若∠BAC=∠BAD,BD⊥BC,请探究∠DAE与∠C的数量关系,写出你的探究结论,并加以证明;
(3)如图3,在(2)的条件下,过点D作DF∥BC交射线于点F,当∠DFE=8∠DAE时,求∠BAD的度数.

-
科目: 来源: 题型:
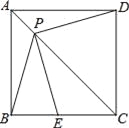
查看答案和解析>>【题目】如图,P是正方形ABCD对角线AC上一点,点E在BC上,且PE=PB.
(1)求证:PE=PD;
(2)连接DE,试判断∠PED的度数,并证明你的结论.
-
科目: 来源: 题型:
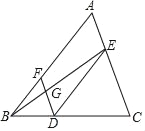
查看答案和解析>>【题目】完成下面的证明:如图,点D,E,F分别是三角形ABC的边BC,CA,AB上的点,连接DE,DF,DE∥AB,∠BFD=∠CED,连接BE交DF于点G,求证:∠EGF+∠AEG=180°.
证明:∵DE∥AB(已知),
∴∠A=∠CED( )
又∵∠BFD=∠CED(已知),
∴∠A=∠BFD( )
∴DF∥AE( )
∴∠EGF+∠AEG=180°( )
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:抛物线y=ax2+bx﹣3经过点A(7,﹣3),与x轴正半轴交于点B(m,0)、C(6m、0)两点,与y轴交于点D.
(1)求m的值;
(2)求这条抛物线的表达式;
(3)点P在抛物线上,点Q在x轴上,当∠PQD=90°且PQ=2DQ时,求点P、Q的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,∠MON=45°,点P是∠MON内一点,过点P作PA⊥OM于点A、PB⊥ON于点B,且PB=2
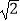 .取OP的中点C,联结AC并延长,交OB于点D.
.取OP的中点C,联结AC并延长,交OB于点D.
(1)求证:∠ADB=∠OPB;
(2)设PA=x,OD=y,求y关于x的函数解析式;
(3)分别联结AB、BC,当△ABD与△CPB相似时,求PA的长.
相关试题

