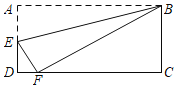
【题目】如图,已知矩形纸片ABCD的两边AB:BC=2:1,过点B折叠纸片,使点A落在边CD上的点F处,折痕为BE.若AB的长为4,则EF的长为( )
A. 8-4![]() B. 2
B. 2![]() C. 4
C. 4![]() 6D.
6D. ![]()
参考答案:
【答案】A
【解析】
由翻折的性质可知:BF=AB=4,AE=EF,设AE=EF=x,在Rt△DEF中,利用勾股定理构建方程即可解决问题.
解:∵AB=4,AB:BC=2:1,
∴BC=2,
∵四边形ABCD是矩形,
∴AD=BC=2,CD=AB=4,∠D=∠C=90°,
由翻折的性质可知:BF=AB=4,AE=EF,设AE=EF=x,
∴CF=![]() ,
,
在Rt△DEF中,
∵DE2+DF2=EF2,
∴(2-x)2+(4-2![]() )2=x2,
)2=x2,
x=8-4![]() .
.
故选A.
-
科目: 来源: 题型:
查看答案和解析>>【题目】武胜县白坪—飞龙乡村旅游度假村橙海阳光景点组织
 辆汽车装运完
辆汽车装运完 三种脐橙共
三种脐橙共 吨到外地销售.按计划,
吨到外地销售.按计划,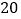 辆汽车都要装运,每辆汽车只能装运同一种脐橙,且必须装满.根据下表提供的信息,解答以下问题:
辆汽车都要装运,每辆汽车只能装运同一种脐橙,且必须装满.根据下表提供的信息,解答以下问题:脐橙品种


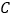
每辆汽车运载量(吨)
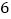
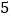
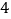
每吨脐橙获得(元)
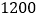
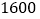
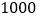
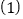 设装运
设装运 种脐橙的车辆数为
种脐橙的车辆数为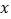 ,装运
,装运 种脐橙的车辆数为
种脐橙的车辆数为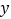 ,求
,求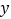 与
与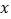 之间的函数关系式;
之间的函数关系式;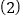 如果装运每种脐橙的车辆数都不少于
如果装运每种脐橙的车辆数都不少于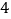 辆,那么车辆的安排方案有几种?
辆,那么车辆的安排方案有几种? 设销售利润为
设销售利润为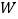 (元),求
(元),求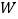 与
与 之间的函数关系式;若要使此次销售获利最大,应采用哪种安排方案?并求出最大利润的值.
之间的函数关系式;若要使此次销售获利最大,应采用哪种安排方案?并求出最大利润的值. -
科目: 来源: 题型:
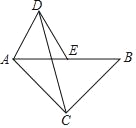
查看答案和解析>>【题目】如图,在等腰Rt△ABC中,∠ACB=90°,AB=4,点E为AB的中点.以AE为边作等边△ADE(点D与点C分别在AB的异侧),连接CD.则△ACD的面积为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,A、B两点分别位于一个池塘的两端,小明想用绳子测量A、B间的距离,但绳子不够长.他叔叔帮他出了一个这样的主意:先在地上取一个可以直接到达A点和B点的点C,连接AC并延长到D,使CD=AC;连接BC并延长到E,使CE=CB;连接DE并测量出它的长度.
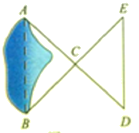
(1)DE=AB吗?请说明理由;
(2)如果DE的长度是8 m,则AB的长度是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD中,AB=20,BC=15,CD=7,AD=24,∠B=90°.
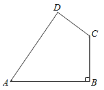
(1)判断∠D是否是直角,并说明理由.
(2)求四边形ABCD的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD为菱形,∠D=60°,AB=4,E为边BC上的动点,连接AE,作AE的垂直平分线GF交直线CD于F点,垂足为点G,则线段GF的最小值为____________.
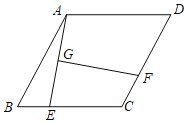
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,一次函数y=kx+b(k≠0)的图象与x轴交于点A,与y轴交于点B(0,2),且与正比例函数y=
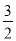 x的图象交于点C(m,3).
x的图象交于点C(m,3).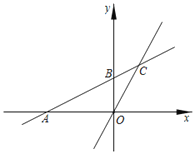
(1)求一次函数y=kx+b(k≠0)的函数关系式;
(2)△AOC的面积为______;
(3)若点M在第二象限,△MAB是以AB为直角边的等腰直角三角形,直接写出点M的坐标.
相关试题

