【题目】如图1,已知△ABC中,∠BAC=90°,AB=AC,AE是过A的一条直线。且点B、C在AE的两侧,BD⊥AE于D,CE⊥AE于E,试设明:
(1)BD=DE+CE;
(2)若直线AE绕A点旋转到图2位置(BD<CE),其余条件不变时,则BD与DE、CE的关系如何?
(3)若直线AE绕A点旋转到图3位置(CE<BD),其余条件不变时,则BD与DE、CE的关系 。(直接写出结果)



参考答案:
【答案】(1)见解析;(2)DE=BD-CE,理由见解析;(3)DE=BD-CE,理由见解析。
【解析】
(1)证明△ABD≌△CAE,即可证得BD=AE,AD=CE,而AE=AD+DE=CE+DE,即可证得;(2)(3)图形变换了,但是(1)中的全等关系并没有改变,因而BD与DE、CE的关系并没有改变,利用(1)的方法即可快速证明。
解:(1)证明:∵∠BAC=90°,
∴∠BAD+∠EAC=90°,
又∵BD⊥AE,CE⊥AE,
∴∠BDA=∠AEC=90°,∠BAD+∠ABD=90°,
·∴∠ABD=∠EAC,
又∵AB=AC,
∴△ABD≌△CAE,
∴BD=AE,AD=CE,
又∵AE=AD+DE=CE+DE,
. ∴BD=DE+CE.
(2)BD=DE-CE,理由如下:
如图2:∵∠BAC=90°,
∴∠BAD+∠EAC=90°,
又∵BD⊥AE,CE⊥AE,
∴∠BDA=∠AEC=90°,∠BAD+∠ABD=90°,
·∴∠ABD=∠EAC,
又∵AB=AC,
∴△ABD≌△CAE,
∴BD=AE,AD=CE,
又∵AE=DE-AD
. ∴BD=DE-CE.
(3) BD=DE-CE,理由如下:
如图3:∵∠BAC=90°,
∴∠BAD+∠EAC=90°,
又∵BD⊥AE,CE⊥AE,
∴∠BDA=∠AEC=90°,∠BAD+∠ABD=90°,
·∴∠ABD=∠EAC,
又∵AB=AC,
∴△ABD≌△CAE,
∴BD=AE,AD=CE,
又∵AE=DE-AD=DE-CE,
. ∴BD=DE-CE.
同理可得,DE=BD+CE;(3)同理可得,DE=BD+CE.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,直线l:y=
 x+m与x轴、y轴分别交于点A和点B(0,﹣1),抛物线y=
x+m与x轴、y轴分别交于点A和点B(0,﹣1),抛物线y= x2+bx+c经过点B,与直线l的另一个交点为C(4,n).
x2+bx+c经过点B,与直线l的另一个交点为C(4,n).(1)求n的值和抛物线的解析式;
(2)点D在抛物线上,DE∥y轴交直线l于点E,点F在直线l上,且四边形DFEG为矩形(如图2),设点D的横坐标为t(0<t<4),矩形DFEG的周长为p,求p与t的函数关系式以及p的最大值;
(3)将△AOB绕平面内某点M旋转90°或180°,得到△A1O1B1,点A、O、B的对应点分别是点A1、O1、B1.若△A1O1B1的两个顶点恰好落在抛物线上,那么我们就称这样的点为“落点”,请直接写出“落点”的个数和旋转180°时点A1的横坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】关于x的方程rx2+(r+2)x+r﹣1=0有根只有整数根的一切有理数r的值有( )个.
A. 1 B. 2 C. 3 D. 不能确定
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的直径,弦CD⊥AB于点G,点F是CD上的一点,且满足
 ,连接AF并延长交⊙O于点E,连接AD、DE,若CF=2,AF=3,给出下列结论:①△ADF∽△AED;②GF=2;③tan∠E=
,连接AF并延长交⊙O于点E,连接AD、DE,若CF=2,AF=3,给出下列结论:①△ADF∽△AED;②GF=2;③tan∠E= ;④S△ADE=7
;④S△ADE=7 .其中正确的是__________(写出所有正确结论的序号).
.其中正确的是__________(写出所有正确结论的序号).
-
科目: 来源: 题型:
查看答案和解析>>【题目】正方形A1B1C1O,A2B2C2C1,A3B3C3C2,…按如图的方式放置,点A1,A2,A3…和点C1,C2,C3…分别在直线y=x+1和x轴上,则点Bn的坐标为_____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】我市某中学有一块四边形的空地ABCD,如图所示,为了绿化环境,学校计划在空地上种植草皮,经测量∠A=90°,AB=3m,DA=4m,BC=12m,CD=13m.
(1)求出空地ABCD的面积.
(2)若每种植1平方米草皮需要200元,问总共需投入多少元?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将边长为4的正方形置于平面直角坐标系第一象限,使AB边落在x轴正半轴上,且点A的坐标是(1,0).

(1)直线y=
 x﹣
x﹣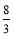 经过点C,且与x轴交于点E,求四边形AECD的面积;
经过点C,且与x轴交于点E,求四边形AECD的面积;(2)若直线l经过点E,且将正方形ABCD分成面积相等的两部分,求直线l的函数表达式.
相关试题

