搜索
【题目】根据不等式的基本性质，把下列不等式化成“x＞a”或“x＜a”的形式：
（1）4x＞3x+5 （2）－2x<17
（3）0.3x＜－0.9 （4）x＜
x－4
参考答案：
【答案】（1）x＞5；（2）x＞
；（3）x＜－3．（4）x＜－8
【解析】分析：（1）直接利用不等式的基本性质1对不等式进行变形即可；（2）利用不等式的基本性质3对不等式变形即可，注意不等号的方向；
（3）利用不等式的基本性质2对不等式变形即可；
（4）先利用不等式的基本性质1对不等式进行变形，再利用不等式的基本性质2对不等式变形即可.
本题解析：
（1）4x＞3x+5
4x-3x＞5，
解得：x＞5；
（2）-2x＜17
解得：x＞-
；
（3）0.3x＜-0.9
解得：x＜-3；
（4）x＜
x-4
x-
x＜-4，
x＜-4，
解得：x＜-8.
-
科目： 来源： 题型：
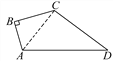
查看答案和解析>>【题目】如图，∠B＝90°，AB＝3，BC＝4，CD＝12，AD＝13.求四边形ABCD的面积．
-
科目： 来源： 题型：
查看答案和解析>>【题目】抛物线y=
+x+m的顶点在直线y=x+3上，过点F（﹣2，2）的直线交该抛物线于点M、N两点（点M在点N的左边），MA⊥x轴于点A，NB⊥x轴于点B．
（1）先通过配方求抛物线的顶点坐标（坐标可用含m的代数式表示），再求m的值；
（2）设点N的横坐标为a，试用含a的代数式表示点N的纵坐标，并说明NF=NB；
（3）若射线NM交x轴于点P，且PAPB=
，求点M的坐标． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在四边形ABCD中，DC∥AB，CB⊥AB，AB=AD，CD=
AB，点E、F分别为AB、AD的中点，则△AEF与多边形BCDFE的面积之比为（ ） 
A.
B.
C.
D.
-
科目： 来源： 题型：
查看答案和解析>>【题目】请阅读求绝对值不等式|x|＜3和|x|＞3的解集的过程：
因为|x|＜3，从如图1所示的数轴上看：大于-3而小于3的数的绝对值是小于3的，所以|x|＜3的解集是-3＜x＜3；
因为|x|＞3，从如图2所示的数轴上看：小大于-3的数和大于3的数的绝对值是大于3的，所以|x|＞3的解集是x＜-3或x＞3．
解答下面的问题：
（1）不等式|x|＜a（a＞0）的解集为______；不等式|x|＞a（a＞0）的解集为______．
（2）解不等式|x-5|＜3；
（3）解不等式|x-3|＞5．
-
科目： 来源： 题型：
查看答案和解析>>【题目】文文和彬彬在证明“有两个角相等的三角形是等腰三角形”这一命题时，画出图形，写出“已知”，“求证”（如图），她们对各自所作的辅助线描述如下：
文文：“过点A作BC的中垂线AD，垂足为D”；
彬彬：“作△ABC的角平分线AD”．
数学老师看了两位同学的辅助线作法后，说：“彬彬的作法是正确的，而文文的作法需要订正．”
（1）请你简要说明文文的辅助线作法错在哪里；
（2）根据彬彬的辅助线作法，完成证明过程．
-
科目： 来源： 题型：
查看答案和解析>>【题目】四边形ABCD是正方形．
(1)如图(1)所示，点G是BC边上任意一点(不与B，C两点重合)，连接AG，作BF⊥AG于点F，DE⊥AG于点E．求证△ABF≌△DAE；
(2)在(1)中，线段EF与AF，BF的等量关系是____；(不需证明，直接写出结论即可)
(3)如图(2)所示，若点G是CD边上任意一点(不与C，D两点重合)，作BF⊥AG于点F，DE⊥AG于点E，那么图中的全等三角形是____，线段EF与AF，BF的等量关系是____．(不需证明，直接写出结论即可)
相关试题
