【题目】如图,用同样规格黑白两色的正方形瓷砖铺设矩形地面,观察下列图形并解答有关问题:
 ……
……
n=1 n=2 n=3
(1)在第n个图中,共有 块白色瓷砖,共有 块黑色瓷砖(均用含n的代数式表示);
(2)设铺设地面所用瓷砖总数为y,请写出y与(1)中的n的函数关系式(不要求写出自变量的取值范围);
(3)若铺设这样的矩形地面共用了506块瓷砖,通过计算求此时n的值;
(4)是否存在n,使得黑瓷砖与白瓷砖块数相等?说明理由.
参考答案:
【答案】(1)n(n+1),4n+6;(2)y=n2+5n+6;(3)20;(4)不存在.
【解析】【试题分析】(1)第1个图形,白色瓷砖有![]() 个,黑色瓷砖有
个,黑色瓷砖有![]() 个;第2个图形中,白色瓷砖有
个;第2个图形中,白色瓷砖有![]() 个,黑色瓷砖有
个,黑色瓷砖有![]() 个;…则第n个图形中,白色瓷砖有
个;…则第n个图形中,白色瓷砖有![]() 个,黑色瓷砖有
个,黑色瓷砖有![]() 个;(2)根据(1)中分析,
个;(2)根据(1)中分析, ![]() ;
;
(3)由题意得: ![]() ,解得n1=20,n2=-25(不合题意,舍去).即n的值为20.
,解得n1=20,n2=-25(不合题意,舍去).即n的值为20.
(4)根据(1)中分析,得n(n+1)=4n+6.解得n1=![]() ,n2=
,n2=![]() ,(不是正整数,都舍去),则不存在n使得黑瓷砖与白瓷砖块数相等.
,(不是正整数,都舍去),则不存在n使得黑瓷砖与白瓷砖块数相等.
【试题解析】
(1)在第n个图中,共有n(n+1)块白色瓷砖,共有4n+6块黑色瓷砖;
(2)y=n2+5n+6.
(3)n2+5n+6=506.
解得n1=20,n2=-25(不合题意,舍去).
∴n的值为20.
(4)由题意,得n(n+1)=4n+6.
解得n1=![]() ,n2=
,n2=![]() (舍去).又因为
(舍去).又因为![]() 不是正整数,
不是正整数,
∴不存在n使得黑瓷砖与白瓷砖块数相等.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某学校为了解学生的课外阅读情况,随机抽取了50名学生,并统计他们平均每天的课外阅读时间t(单位:min),然后利用所得数据绘制成如下不完整的统计表.
课外阅读时间t
频数
百分比
10≤t<30
4
8%
30≤t<50
8
16%
50≤t<70
a
40%
70≤t<90
16
b
90≤t<110
2
4%
合计
50
100%
请根据图表中提供的信息回答下列问题:
(1)a= ,b= ;
(2)将频数分布直方图补充完整;
(3)若全校有900名学生,估计该校有多少学生平均每天的课外阅读时间不少于50min?

-
科目: 来源: 题型:
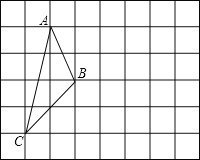
查看答案和解析>>【题目】如图,在方格纸中,每个小正方形的边长均为1个单位长度有一个△ABC,它的三个顶点均与小正方形的顶点重合.
(1)将△ABC向右平移3个单位长度,得到△DEF(A与D、B与E、C与F对应),请在方格纸中画出△DEF;
(2)在(1)的条件下,连接AE和CE,请直接写出△ACE的面积S,并判断B是否在边AE上.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1) 如图1,正方形ABCD的边长为5,点E是AB上一点,点F是AD延长线上一点,且BE=DF,四边形AEGF是矩形,写出矩形AEGF的面积y与BE的长x之间的函数关系式;
(2) 如图2,已知一长方形打印纸长20 cm,宽15 cm,现在要在打印纸上打印文稿,上下左右各留出一定距离.设留出的距离均为x cm,打印文稿面积为y cm2,试写出y与x之间的关系式,并求出x的取值范围.
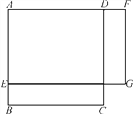
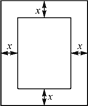
图1 图2
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法中正确的是( ).
A. “打开电视机,正在播放《动物世界》”是必然事件
B. 某种彩票的中奖概率为
 ,说明每买1000张,一定有一张中奖
,说明每买1000张,一定有一张中奖C. 抛掷一枚质地均匀的硬币一次,出现正面朝上的概率为

D. 想了解长沙市所有城镇居民的人均年收入水平,宜采用抽样调查
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市居民用电的电价实行阶梯收费,收费标准如下表:
一户居民每月用电量x(单位:度)
电费价格(单位:元/度)
0<x≤200
a
200<x≤400
b
x>400
0.92
(1)已知李叔家四月份用电286度,缴纳电费178.76元;五月份用电316度,缴纳电费198.56元,请你根据以上数据,求出表格中a,b的值.
(2)六月份是用电高峰期,李叔计划六月份电费支出不超过300元,那么李叔家六月份最多可用电多少度?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
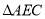 ≌
≌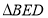 ,点
,点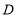 在
在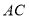 边上,
边上,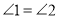 ,
,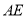 和
和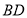 相交于点
相交于点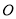 .下列说法:
.下列说法:(1)若
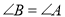 ,则
,则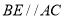 ;
;(2)若
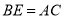 ,则
,则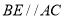 ;
;(3)若
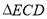 ≌
≌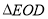 ,
,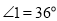 ,则
,则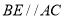 .
.其中正确的有( )个.
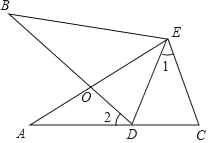
A. 3个B. 2个C. 1个D. 0个
相关试题

