Question

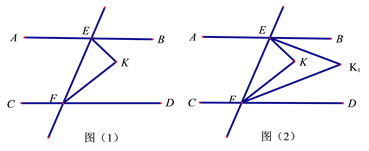
【题目】已知：如图(1)，直线AB∥CD，EF分别交AB、CD于E、F两点，∠BEF、∠DFE的平分线相交于点K．（1）求∠EKF的度数．（计算过程不准用三角形内角和）（2）如图(2)，∠BEK、∠DFK的平分线相交于点K1，问∠K1与∠K的度数是否存在某种特定的等量关系？写出结论并证明．（3）在图2中作∠BEK1、∠DFK1的平分线相交于点K2，作∠BEK2、∠DFK2的平分线相交于点K3，依此类推，作∠BEKn、∠DFKn的平分线相交于点Kn+1，请用含的n式子表示∠Kn+1的度数．（直接写出答案，不必写解答过程）

Answer 1

【答案】（1）∠EKF=90°；（2）∠K=2∠K1理由见解析；（3）归纳总结得：∠Kn+1= ×90°．

【解析】试题分析：（1）过K作KG∥AB，可得KG∥CD，可得出两对内错角相等，由EK与FK分别为角平平分线，利用角平分线定义得到两对角相等，再由AB与CD平行，利用两直线平行同旁内角互补得到两对角互补，利用等式的性质求出∠BKE+∠DFK的度数，即可求出∠EKF的度数；（2）∠K=2∠K1，由∠BEK、∠DFK的平分线相交于点K1，利用角平分线定义得到两对角相等，等量代换求出∠K1，进而确定出两角的关系；（3）依此类推即可确定出∠Kn+1的度数；

试题解析：

（1）过K作KG∥AB，可得KG∥CD，如图所示：

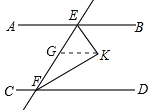
∴∠BEK=∠EKG，∠GKF=∠KFD，

∵EK、FK分别为∠BEF与∠EFD的平分线，

∴∠BEK=∠FEK，∠EFK=∠DFK，

∵AB∥CD，

∴∠BEK+∠FEK+∠EFK+∠DFK=180°，即2（∠BEK+∠DFK）=180°，

∴∠BEK+∠DFK=90°，则∠EKF=∠EKG+∠GKF=90°；

（2）∠K=2∠K1，理由为：

∵∠BEK、∠DFK的平分线相交于点K1，

∴∠BEK1=∠KEK1，∠KFK1=∠DFK1，

∵∠BEK+∠FEK+∠EFK+∠DFK=180°，即2（∠BEK+∠KFD）=180°，

∴∠BEK+∠KFD=90°，即∠KEK1+∠KFK1=45°，

∴∠K1=180°-（∠KEF+∠EFK）-（∠KEK1+∠KFK1）=45°，则∠K=2∠K1；

（3）归纳总结得：∠Kn+1= ×90°。