【题目】如图,在平面直角坐标系xOy中,一次函数y=k1x+b的图象与x轴交于点A(-3,0),与y轴交于点B,且与正比例函数y=kx的图象交点为C(3,4).
(1)求正比例函数与一次函数的关系式;
(2)若点D在第二象限,△DAB是以AB为直角边的等腰直角三角形,请求出点D的坐标;
(3)在x轴上是否存在一点E使△BCE周长最小,若存在,求出点E的坐标
(4)在x轴上求一点P使△POC为等腰三角形,请直接写出所有符合条件的点P的坐标.

参考答案:
【答案】(1)一次函数关系式为y=![]() x+2,正比例函数关系式为y=
x+2,正比例函数关系式为y=![]() x;
x;
(2)D2(-2,5) ;
(3)存在,E点的坐标为(1,0);
(4)P(5,0),P(-5,0),P (6, 0),P (![]() ,0)
,0)
【解析】试题分析:(1)根据待定系数法即可解决.
(2)分两种情形讨论,添加辅助线构造全等三角形即可求出点![]() 坐标.
坐标.
![]() 存在;作
存在;作![]() 关于
关于![]() 轴对称点
轴对称点![]() ,连接
,连接![]() ,交
,交![]() 轴于
轴于![]() ,此时
,此时![]() 周长最小.求出点
周长最小.求出点![]() 的坐标.
的坐标.
(4)分![]() 三种情形研究即可.
三种情形研究即可.
试题解析:(1)∵正比例函数y=kx的图象经过点C(3,4),
∴4=3k,
![]()
∴正比例函数为![]()
∵一次函数![]() 的图象经过A(3,0),C(3,4)
的图象经过A(3,0),C(3,4)
![]()
解得: 
∴一次函数为![]()
(2)①当DA⊥AB时,作DM⊥x轴垂足为M,
![]()
∴∠DAM=∠ABO,
∵DA=AB,∠DMA=∠AOB,
![]()
∴DM=AO=3,AM=BO=2,
∴D(5,3),
②当D′B⊥AB时,作D′N⊥y轴垂足为N,
同理得![]()
∴D′N=BO=2,BN=AO=3,
∴D′(2,5)
∴D点坐标为(5,3)或(2,5).

(3)存在;作![]() 关于
关于![]() 轴对称点
轴对称点![]() ,连接
,连接![]() ,交
,交![]() 轴于
轴于![]() ,此时
,此时![]() 周长最小.
周长最小.
![]()
解得: ![]()
![]() 的解析式为:
的解析式为: ![]()
令![]() 得
得![]()
解得: ![]()
∴点![]() 的坐标为
的坐标为![]()
![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知∠A=40°,则它的余角为( )
A.40°
B.50°
C.130°
D.140° -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,一次函数y1=kx+b的图象与反比例函数y2=
 的图象交于A(﹣2,n),B(1,﹣3)两点.
的图象交于A(﹣2,n),B(1,﹣3)两点.(1)试确定上述一次函数和反比例函数的表达式;
(2)求△AOB的面积;

-
科目: 来源: 题型:
查看答案和解析>>【题目】我国是一个严重缺水的国家.为了加强公民的节水意识,某市制定了如下用水收费标准:每户每月的用水不超过6吨时,水价为每吨2元,超过6吨时,超过的部分按每吨3元收费.该市某户居民5月份用水x吨,应交水费y元.
(1)若0<x≤6,请写出y与x的函数关系式.
(2)若x>6,请写出y与x的函数关系式.
(3)如果该户居民这个月交水费27元,那么这个月该户用了多少吨水?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知实数a、b、c满足a+b=ab=c,有下列结论:
①若c≠0,则
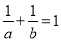 ;②若a=3,则b+c=9;
;②若a=3,则b+c=9;③若a=b=c,则abc=0;④若a、b、c中只有两个数相等,则a+b+c=8.
其中正确的是 _____________ (把所有正确结论的序号都选上).
-
科目: 来源: 题型:
查看答案和解析>>【题目】在正三角形、正方形、正五边形、正六边形中不能镶嵌成一个平面图案的是 .
-
科目: 来源: 题型:
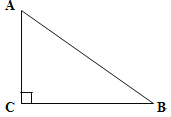
查看答案和解析>>【题目】如图,已知△ABC,∠C=90,AC<BC,D为BC上一点,且到A,B两点的距离相等.
(1)用直尺和圆规,作出点D的位置(不写作法,保留作图痕迹);
(2)连结AD,若∠B=37°,则∠CAD=_________度.
相关试题

