【题目】如图,已知点A(0,2),B(2,2),C(﹣1,﹣2),抛物线F:y=x2﹣2mx+m2﹣2与直线x=﹣2交于点P.
(1)当抛物线F经过点C时,求它的表达式;
(2)设点P的纵坐标为yP,求yP的最小值,此时抛物线F上有两点(x1,y1),(x2,y2),且x1<x2≤﹣2,比较y1与y2的大小;
(3)当抛物线F与线段AB有公共点时,直接写出m的取值范围.

参考答案:
【答案】(1)y=x2+2x﹣1;(2) y1>y2;(3) ﹣2≤m≤0或2≤m≤4.
【解析】试题分析:
(1)根据抛物线F:y=x2﹣2mx+m2﹣2过点C(﹣1,﹣2),可以求得抛物线F的表达式;
(2)根据题意,可以求得yP的最小值和此时抛物线的表达式,从而可以比较y1与y2的大小;
(3)根据题意可以列出相应的不等式组,从而可以解答本题.
试题解析:
(1)∵抛物线F经过点C(﹣1,﹣2),
∴﹣2=(﹣1)2﹣2×m×(﹣1)+m2﹣2,
解得,m=﹣1,
∴抛物线F的表达式是:y=x2+2x﹣1;
(2)当x=﹣2时,yp=4+4m+m2﹣2=(m+2)2﹣2,
∴当m=﹣2时,yp的最小值﹣2,
此时抛物线F的表达式是:y=x2+4x+2=(x+2)2﹣2,
∴当x≤﹣2时,y随x的增大而减小,
∵x1<x2≤﹣2,
∴y1>y2;
(3)m的取值范围是﹣2≤m≤0或2≤m≤4,
理由:∵抛物线F与线段AB有公共点,点A(0,2),B(2,2),
∴![]() 或
或![]() 或
或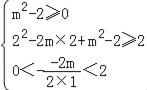 ,
,
解得,﹣2≤m≤0或2≤m≤4.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,点P(﹣3,2)在 ( )
A.第一象限
B.第二象限
C.第三象限
D.第四象限 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD和矩形PEFG中,AB=8,BC=6,PE=2,PG=4.PE与AC交于点M,EF与AC交于点N,动点P从点A出发沿AB以每秒1个单位长的速度向点B匀速运动,伴随点P的运动,矩形PEFG在射线AB上滑动;动点K从点P出发沿折线PE﹣﹣EF以每秒1个单位长的速度匀速运动.点P、K同时开始运动,当点K到达点F时停止运动,点P也随之停止.设点P、K运动的时间是t秒(t>0).
(1)当t=1时,KE=_____,EN=_____;
(2)当t为何值时,△APM的面积与△MNE的面积相等?
(3)当点K到达点N时,求出t的值;
(4)当t为何值时,△PKB是直角三角形?

-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法正确的是( )
A.﹣3是﹣9的平方根
B.3是(﹣3)2的算术平方根
C.(﹣2)2的平方根是2
D.8的立方根是±2 -
科目: 来源: 题型:
查看答案和解析>>【题目】当x=3、y=1时,代数式(x+y)(x﹣y)+y2的值是________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,等腰三角形ABC中,AB=AC,D、E都在BC上,要使△ABD≌△ACE,需要添加一个条件,某学习小组在讨论这个条件时给出了如下几种方案: ①AD=AE;②BD=CE;③BE=CD;④∠BAD=∠CAE,其中可行的有( )
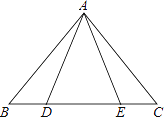
A. 1种 B. 2种 C. 3种 D. 4种
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,已知四边形DOBC是矩形,且D(0,4),B(6,0).若反比例函数y=
 (x>0)的图象经过线段OC的中点A,交DC于点E,交BC于点F.设直线EF的解析式为y=k2x+b.
(x>0)的图象经过线段OC的中点A,交DC于点E,交BC于点F.设直线EF的解析式为y=k2x+b.(1)求反比例函数和直线EF的解析式;
(2)求△OEF的面积;
(3)请结合图象直接写出不等式k2x+b﹣
 >0的解集.
>0的解集.
相关试题

