Question

【题目】某蔬菜经销商去蔬菜生产基地批发某种蔬菜，已知这种蔬菜的批发量在20千克～60千克之间（含20千克和60千克）时，每千克批发价是5元；若超过60千克时，批发的这种蔬菜全部打八折，但批发总金额不得少于300元．

（1）根据题意，填写如表：

蔬菜的批发量（千克）	…	25	60	75	90	…
所付的金额（元）	…	125	300			…

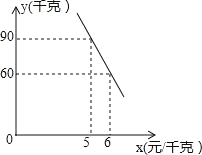
（2）经调查，该蔬菜经销商销售该种蔬菜的日销售量y（千克）与零售价x（元/千克）是一次函数关系，其图象如图，求出y与x之间的函数关系式；

（3）若该蔬菜经销商每日销售此种蔬菜不低于75千克，且当日零售价不变，那么零售价定为多少时，该经销商销售此种蔬菜的当日利润最大？最大利润为多少元？

Answer 1

【答案】(1)填表见解析；（2）y=-30x+240；（3）当x=5.5时，当日可获得利润最大，最大利润为112.5元．

【解析】

试题分析：（1）根据这种蔬菜的批发量在20千克～60千克之间（含20千克和60千克）时，每千克批发价是5元，可得60×5=300元；若超过60千克时，批发的这种蔬菜全部打八折，则90×5×0.8=360元；

（2）把点（5，90），（6，60）代入函数解析式y=kx+b（k≠0），列出方程组，通过解方程组求得函数关系式；

（3）利用最大利润=y（x-4），进而利用配方法求出函数最值即可．

试题解析：（1）由题意知：当蔬菜批发量为60千克时：60×5=300（元），当蔬菜批发量为90千克时：90×5×0.8=360（元），

填写表格如下：

蔬菜的批发量（千克）	…	25	60	75	90	…
所付的金额（元）	…	125	300	300	360	…

（2）设该一次函数解析式为y=kx+b（k≠0），

把点（5，90），（6，60）代入，得，

解得：．

故该一次函数解析式为：y=-30x+240；

（3）设当日可获利润w（元），日零售价为x元，由（2）知，

w=（-30x+240）（x-5×0.8）=-30（x-6）2+120，

∵-30x+240≥75，即x≤5.5，

∴当x=5.5时，当日可获得利润最大，最大利润为112.5元．