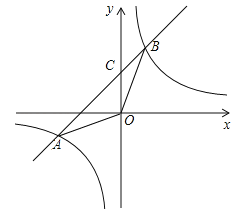
【题目】如图,在平面直角坐标系xOy中,一次函数y=﹣ax+b的图象与反比例函数![]() 的图象相交于点A(﹣4,﹣2),B(m,4),与y轴相交于点C.
的图象相交于点A(﹣4,﹣2),B(m,4),与y轴相交于点C.
(1)求反比例函数和一次函数的表达式;
(2)求点C的坐标及△AOB的面积.

参考答案:
【答案】(1)![]() ,y=x+2;(2)C(0,2),6.
,y=x+2;(2)C(0,2),6.
【解析】
试题分析:(1)由点A的坐标利用反比例函数图象上点的坐标特征即可求出k值,从而得出反比例函数表达式,再由点B的坐标和反比例函数表达式即可求出m值,结合点A、B的坐标利用待定系数法即可求出一次函数表达式;
(2)令一次函数表达式中x=0求出y值即可得出点C的坐标,利用分解图形求面积法结合点A、B的坐标即可得出结论.
试题解析:(1)∵点A(﹣4,﹣2)在反比例函数![]() 的图象上,∴k=﹣4×(﹣2)=8,∴反比例函数的表达式为
的图象上,∴k=﹣4×(﹣2)=8,∴反比例函数的表达式为![]() ;
;
∵点B(m,4)在反比例函数![]() 的图象上,∴4m=8,解得:m=2,∴点B(2,4).
的图象上,∴4m=8,解得:m=2,∴点B(2,4).
将点A(﹣4,﹣2)、B(2,4)代入y=﹣ax+b中,得:![]() ,解得:
,解得:![]() ,∴一次函数的表达式为y=x+2.
,∴一次函数的表达式为y=x+2.
(2)令y=x+2中x=0,则y=2,∴点C的坐标为(0,2),∴S△AOB=![]() OC×(xB﹣xA)=
OC×(xB﹣xA)=![]() ×2×[2﹣(﹣4)]=6.
×2×[2﹣(﹣4)]=6.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某电子产品经过11月、12月连续两次降价,售价由3900元降到了2500元.设平均每月降价的百分率为x,根据题意列出的方程是( )
A. 3900(1+x)2=2500 B. 3900(1﹣x)2=2500
C. 3900(1﹣2x)=2500 D. 2500(1+x)2=3900
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知x1和x2是关于x的方程x2﹣2(m+1)x+m2+3=0的两实数根,x12+x22=22, 则m的值是( )
A. ﹣6或2 B. 2 C. ﹣2 D. 6或﹣2
-
科目: 来源: 题型:
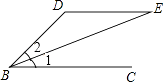
查看答案和解析>>【题目】如图,DE∥BC,∠D:∠DBC=2:1,∠1=∠2,求∠DEB的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若a2=25,|b|=3,则a+b的值是( )
A.﹣8
B.±8
C.±2
D.±8或±2 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的一元二次方程(a﹣1)x2﹣2x+1=0有两个不相等的实数根,则a的取值范围是( )
A.a<2
B.a>2
C.a<﹣2
D.a<2且a≠1 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一条直线分别与直线BE、直线CE、直线BF、直线CF相交于点A,G,H,D且∠1=∠2,∠B=∠C
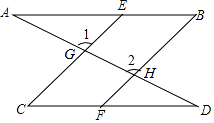
(1)找出图中相互平行的线,说说它们之间为什么是平行的;
(2)证明:∠A=∠D.
相关试题

