搜索
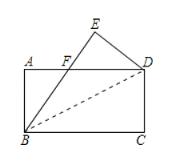
【题目】如图，将矩形
(
)沿
折叠后，点
落在点
处，且
交
于点
，若
，
.
(1)求
的长；
(2)求
和
的面积；
(3)求中点到边上的距离.
参考答案：
【答案】(1)DF=5；(2)S△DBF=10；S△DEF=6；(3)
.
【解析】
（1）易证BF=FD，在直角△ABF中，根据勾股定理就可以求出DF的长；
（2）由折叠的性质得BE=BC=8，DE=CD=4，∠E=90°，EF=BE-BF=3，由S△DEF=
EFDE，S△DBF=S△BDE-S△DEF即可得出结果；
（3）由勾股定理得出BD=
，设F到BD边上的距离为h，则S△DBF= BDh，即可得出结果．
解：(1)∵四边形
是矩形
∴
，
，
，
∴
由折叠性质得：
，
∴
∴
设
，则
在
中，由勾股定理得：
即：
，解得：
，
∴
(2)由折叠的性质得：
，
，
，
，
∴
(3)
设
到
边上的距离为
则
，即：
，解得：
∴到边上的距离为
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，一次函数y=kx+b分别交y轴、x轴于C、D两点，与反比例函数y=
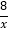（x＞0）的图象交于A（m，8），B（4，n）两点．（1）求一次函数的解析式；
（2）根据图象直接写出kx+b﹣
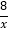＜0的x的取值范围；（3）求△AOB的面积．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，直线PC交⊙O于A，C两点，AB是⊙O的直径，AD平分∠PAB交⊙O于点D，过D作DE垂直PA，垂足为E．
（1）求证：DE是⊙O的切线；
（2）若AE=1，AC=4，求直径AB的长．
-
科目： 来源： 题型：
查看答案和解析>>【题目】在
中，
，
，
，点
为射线
上一点，当
为等腰三角形时，的周长为 _______． -
科目： 来源： 题型：
查看答案和解析>>【题目】已知：△ABC是等腰三角形，动点P在斜边AB所在的直线上，以PC为直角边作等腰三角形PCQ，其中∠PCQ=90°，探究并解决下列问题：
（1）如图①，若点P在线段AB上，且AC=1+
，PA=
，则：①线段PB= ，PC= ；
②猜想：PA2，PB2，PQ2三者之间的数量关系为 ；
（2）如图②，若点P在AB的延长线上，在（1）中所猜想的结论仍然成立，请你利用图②给出证明过程；
（3）若动点P满足
，求
的值．（提示：请利用备用图进行探求） 
-
科目： 来源： 题型：
查看答案和解析>>【题目】一位运动员在距篮下4m处跳起投篮，球运行的路线是抛物线，当球运行的水平距离是2.5m时，达到最大高度3.5m，然后准确落入篮圈．已知篮圈中心到地面的距离为3.05m．
（1）建立如图所示的平面直角坐标系，求抛物线的解析式．
（2）该运动员身高1.8m，在这次跳投中，球在头顶上0.25m处出手，
问：球出手时，他距离地面的高度是多少？
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，将三角形纸片ABC沿AD折叠，使点C落在BD边上的点E处．若BC＝8，BE＝2．则AB2﹣AC2的值为（ ）
A. 4 B. 6 C. 10 D. 16
相关试题
