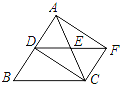
【题目】如图,已知⊙O的半径为1,AC是⊙O的直径,过点C作⊙O的切线BC,E是BC的中点,AB交⊙O于D点. 
(1)直接写出ED和EC的数量关系:;
(2)DE是⊙O的切线吗?若是,给出证明;若不是,说明理由;
(3)填空:当BC=时,四边形AOED是平行四边形,同时以点O、D、E、C为顶点的四边形是 .
参考答案:
【答案】
(1)ED=EC
(2)解:DE是⊙O的切线.理由如下:
连结OD,如图,
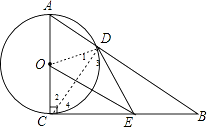
∵BC为切线,
∴OC⊥BC,
∴∠OCB=90°,即∠2+∠4=90°,
∵OC=OD,ED=EC,
∴∠1=∠2,∠3=∠4,
∴∠1+∠3=∠2+∠4=90°,即∠ODB=90°,
∴OD⊥DE,
∴DE是⊙O的切线
(3)2;正方形
【解析】解:(1.)连结CD,如图, 
∵AC是⊙O的直径,
∴∠ADC=90°,
∵E是BC的中点,
∴DE=CE=BE;
(3.)当BC=2时,
∵CA=CB=2,
∴△ACB为等腰直角三角形,
∴∠B=45°,
∴△BCD为等腰直角三角形,
∴DE⊥BC,DE= ![]() BC=1,
BC=1,
∵OA=DE=1,AO∥DE,
∴四边形AOED是平行四边形;
∵OD=OC=CE=DE=1,∠OCE=90°,
∴四边形OCED为正方形.
所以答案是ED=EC;2,正方形.
【考点精析】掌握平行四边形的判定与性质是解答本题的根本,需要知道若一直线过平行四边形两对角线的交点,则这条直线被一组对边截下的线段以对角线的交点为中点,并且这两条直线二等分此平行四边形的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法:①平角就是一条直线;②直线比射线线长;③平面内三条互不重合的直线的公共点个数有0个、1个、2个或3个;④连接两点的线段叫两点之间的距离;⑤两条射线组成的图形叫做角;⑥一条射线把一个角分成两个角,这条射线是这个角的角平分线,其中正确的有( )
A. 0个 B. 1个 C. 2个 D. 3个
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列定义一种关于n的运算:①当n是奇数时,结果为3n+5 ②n为偶数时结果是
 (其中k是使
(其中k是使 是奇数的正整数),并且运算重复进行.例如:取n=26,则…,若n=449,则第449次运算结果是( )
是奇数的正整数),并且运算重复进行.例如:取n=26,则…,若n=449,则第449次运算结果是( )A. 1 B. 2 C. 7 D. 8
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,有一张长40cm,宽30cm的长方形硬纸片,截去四个小正方形之后,折成如图2所示的无盖纸盒,设无盖纸盒高为xcm.
 用关于x的代数式分别表示无盖纸盒的长和宽.
用关于x的代数式分别表示无盖纸盒的长和宽. 若纸盒的底面积为
若纸盒的底面积为 ,求纸盒的高.
,求纸盒的高. 现根据
现根据 中的纸盒,制作了一个与下底面相同大小的矩形盒盖,并在盒盖上设计了六个总面积为
中的纸盒,制作了一个与下底面相同大小的矩形盒盖,并在盒盖上设计了六个总面积为 的矩形图案
的矩形图案 如图3所示
如图3所示 ,每个图案的高为ycm,A图案的宽为xcm,之后图案的宽度依次递增1cm,各图案的间距、A图案与左边沿的间距、F图案与右边沿的间距均相等,且不小于
,每个图案的高为ycm,A图案的宽为xcm,之后图案的宽度依次递增1cm,各图案的间距、A图案与左边沿的间距、F图案与右边沿的间距均相等,且不小于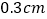 ,求x的取值范围和y的最小值.
,求x的取值范围和y的最小值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 中,
中, ,
, ,DF是
,DF是 的中位线,点C关于DF的对称点为E,以DE,EF为邻边构造矩形DEFG,DG交BC于点H,连结CG.
的中位线,点C关于DF的对称点为E,以DE,EF为邻边构造矩形DEFG,DG交BC于点H,连结CG. 求证:
求证: ≌
≌ .
. 若
若 .
. 求CG的长.
求CG的长. 在
在 的边上取一点P,在矩形DEFG的边上取一点Q,若以P,Q,C,G为顶点的四边形是平行四边形,求出所有满足条件的平行四边形的面积.
的边上取一点P,在矩形DEFG的边上取一点Q,若以P,Q,C,G为顶点的四边形是平行四边形,求出所有满足条件的平行四边形的面积. 在
在 内取一点O,使四边形AOHD是平行四边形,连结OA,OB,OC,直接写出
内取一点O,使四边形AOHD是平行四边形,连结OA,OB,OC,直接写出 ,
, ,
, 的面积之比.
的面积之比.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,菱形ABCD的顶点A的坐标为(2,0),点B的坐标为(0,1),点C在第一象限,对角线BD与x轴平行.直线y=x+4与x轴、y轴分别交于点E,F.将菱形ABCD沿x轴向左平移k个单位,当点C落在△EOF的内部时(不包括三角形的边),k的值可能是( )

A.2 B.3 C.4 D.5
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△BC中,AC=BC,点D、E分别是边AB、AC的中点.延长DE到点F,使DE=EF,得四边形ADCF.若使四边形ADCF是正方形,则应在△ABC中再添加一个条件为_____.
相关试题

