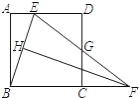
【题目】如图,在正方形ABCD中,点E是AD上的点,点F是BC的延长线上一点,CF=DE,连结BE和EF,EF与CD交于点G,且∠FBE=∠FEB.
(1)过点F作FH⊥BE于点H,证明:![]() ;
;
(2)猜想:BE、AE、EF之间的数量关系,并证明你的结论;
(3)若DG=2,求AE值.
参考答案:
【答案】(1)证明见解析;(2)证明见解析;(3)![]()
【解析】试题分析:(1)根据正方形的性质得到∠AEB=∠EBF,由已知条件得到∠A=∠BHF,根据相似三角形的判定定理即可得到结论;
(2)根据已知条件得到FH是等腰△FBE底边上的高,求得BH=![]() BE,由根据相似三角形的性质得到
BE,由根据相似三角形的性质得到![]() ;
;
(3)由已知条件得到正方形ABCD的边长为2,设AE=k(0<k<2),则DE═2-k,BF=4-k,根据勾股定理列方程即可得到结果.
试题解析:(1)证明:∵在正方形ABCD中,AD∥BC,
∴∠AEB=∠EBF,
又∵FH⊥BE,∴∠A=∠BHF=90°,
∴△ABE∽△HFB;
(2)BE2=2AEEF
证明如下:∵∠FBE=∠FEB,∴BF=EF,
∵FH⊥BE,
∴FH是等腰△FBE底边上的中线,
∴BH=![]() BE,
BE,
由(1)得, ![]() ,
,
∴
∴BE2=2AEBF;
∵BF=EF,∴BE2=2AEEF;
(3)解:∵DG═2,
∴正方形ABCD的边长为4,
设AE=k(0<k<4),则DE═4﹣k,BF=8﹣k,
∴在Rt△ABM中,BE2=AB2+AE2=16+k2,
由BE2=2AEBF,得16+k2=2k(8﹣k),
即3k2﹣16k+16=0,解得k1=![]() ,k2=4
,k2=4
∵k≠4,
∴AE=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】点P(-2,1)关于x轴的对称点的坐标为( )
A. (2,1) B. (-2,-1)
C. (2,-1) D. (1,-2)
-
科目: 来源: 题型:
查看答案和解析>>【题目】十边形的内角和为( )
A.360°
B.1440°
C.1800°
D.2160° -
科目: 来源: 题型:
查看答案和解析>>【题目】甲乙两人在同一条道路上同时出发,同时行进,甲步行,乙骑车,出发时甲在前,乙在后,图中l甲,l乙,分别表示出发后甲、乙离出发地的路程s(km)和经历的时间t(h)的关系.

(1)乙出发时甲、乙相距___km.
(2)乙骑行一段路后,自行车发生故障,进行修理,所用的时间是___h.
(3)图象l甲,l乙相交的实际意义是什么?
(4)若乙的自行车没有故障,保持出发时的速度前进,求甲,乙相遇的时间和地点.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了绿化环境,育英中学八年级三班同学都积极参加植树活动,今年植树节时,该班同学植树情况的部分数据如图所示,请根据统计图信息,回答下列问题:
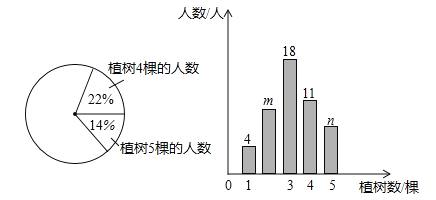
(1)八年级三班共有多少名同学?
(2)条形统计图中,m= ,n= .
(3)扇形统计图中,试计算植树2棵的人数所对应的扇形圆心角的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知四个数:2,﹣3,﹣4,5,任取其中两个数相乘,所得积的最大值是( )
A.20
B.12
C.10
D.﹣6 -
科目: 来源: 题型:
查看答案和解析>>【题目】将点A向右平移2个单位,再向下平移3个单位,得到点A′(4,5),则点A的坐标是_____.
相关试题

