【题目】如图,在△ABC中,点D为边BC的中点,过点A作射线AE,过点C作CF⊥AE于点F,过点B作BG⊥AE于点G,连接FD并延长,交BG于点H.
(1)求证:DF=DH;
(2)若∠CFD=120°,求证:△DHG为等边三角形.

参考答案:
【答案】(1)证明见解析;(2)证明见解析.
【解析】试题
(1)首先证明∠1=∠2,再证明△DCF≌△DBH即可得到DF=DH;
(2)首先根据角的和差关系可以计算出∠GFH=30°,再由∠BGM=90°可得∠GHD=60°,再根据直角三角形的性质可得,HG=![]() HF,进而得到结论.
HF,进而得到结论.
试题解析:(1)∵CF⊥AE,BG⊥AE,
∴∠BGF=∠CFG=90°,
∴∠1+∠GMB=∠2+∠CME,
∵∠GMB=∠CME,
∴∠1=∠2,
∵点D为边BC的中点,
∴DB=CD,
在△BHD和△CED中,
∴△BHD≌△CED(ASA),
∴DF=DH;
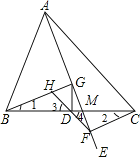
(2)∵∠CFD=120°,∠CFG=90°,
∴∠GFH=30°,
∵∠BGM=90°,
∴∠GHD=60°,
∵△HGF是直角三角形,HD=DF,
∴DG=![]() HF=DH,
HF=DH,
∴△DHG为等边三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)在直角坐标系中,先描出点A(1,3),点B(4,1).并直接写出点A关于x轴的对称的A1的坐标A1 ( , ).
(2)在x轴上找一点C,使AC+BC的值最小; (保留作图痕迹).
(3)用尺规在x轴上找一点P,使PA=PB(保留作图痕迹).

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠C=90°,AE是△ABC的角平分线;ED平分∠AEB交AB于点D;∠CAE=∠B.
(1)如果AC=3.5 cm,求AB的长度;
(2)猜想:ED与AB的位置关系,并证明你的猜想。

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,AD是△ABC的内角平线,交BC于D点,DE⊥AB,DF⊥AC,垂足分别为E、F,连结EF,
(1)请根据上述几何语言,画出完整的图形,作∠BAC的角平分线AD要求尺规作图,(保留作图痕迹,不写作法);
(2)判断AD是否为EF的垂直平分线,并说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】若两条抛物线的顶点相同,则称它们为“友好抛物线”,抛物线C1:y1=﹣2x2+4x+2与C2:y2=﹣x2+mx+n为“友好抛物线”.

(1)求抛物线C2的解析式.
(2)点A是抛物线C2上在第一象限的动点,过A作AQ⊥x轴,Q为垂足,求AQ+OQ的最大值.
(3)设抛物线C2的顶点为C,点B的坐标为(﹣1,4),问在C2的对称轴上是否存在点M,使线段MB绕点M逆时针旋转90°得到线段MB′,且点B′恰好落在抛物线C2上?若存在求出点M的坐标,不存在说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】在同一直角坐标系中,函数y=mx+m和y=﹣mx2+2x+2(m是常数,且m≠0)的图象可能是( )
A.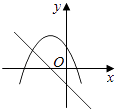
B.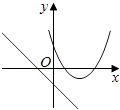
C.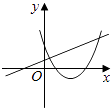
D.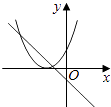
-
科目: 来源: 题型:
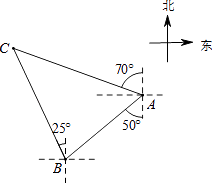
查看答案和解析>>【题目】如图,轮船在A处观测灯塔C位于北偏西70°方向上,轮船从A处以每小时20海里的速度沿南偏西50°方向匀速航行,1小时后到达码头B处,此时,观测灯塔C位于北偏西25°方向上,则灯塔C与码头B的距离是( )
A.10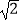 海里
海里
B.10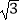 海里
海里
C.10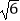 海里
海里
D.20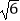 海里
海里
相关试题

