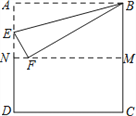
【题目】如图,把正方形纸片ABCD沿对边中点所在的直线对折后展开,折痕为MN,再过点B折叠纸片,使点A落在MN上的点F处,折痕为BE.若AB的长为2,求:
(1) FN的长;
(2) EN的长.(结果保留根号)
参考答案:
【答案】(1) ![]() ;(2)
;(2) ![]() .
.
【解析】试题分析:(1)根据翻折不变性,AB=FB=2,BM=1,在Rt△BFM中,可利用勾股定理求出FM的值,进而可求出FN的长;
(2)根据翻折不变性,AE=EF,在Rt△EFN中,可利用勾股定理求出EF的值,
试题解析:∵四边形ABCD为正方形,AB=2,过点B折叠纸片,使点A落在MN上的点F处,
∴FB=AB=2,BM=1,
则在Rt△BMF中,
FM=![]() =
=![]() ,
,
FN=NM-FM=![]() ;
;
(2)设EN=x,则AE=EF=1-x,
在Rt△EFN中,由勾股定理,得EN2+ F N 2=EF2,即(1-x)2+(![]() )2=x2,
)2=x2,
解得x=![]() .
.
即EN=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若a>b成立,则下列不等式成立的是( )
A. ﹣a>﹣b B. ﹣a+1>﹣b+1 C. a﹣1>b﹣1 D. ﹣(a﹣1)>﹣(b﹣1)
-
科目: 来源: 题型:
查看答案和解析>>【题目】一次数学测验中,某小组五位同学的成绩分别是:110,105,90,95,90,则这五个数据的中位数是( )
A.90
B.95
C.100
D.105 -
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算正确的是( )
A.a2a3=a6
B.(﹣a3)2=﹣a6
C.(ab)2=ab2
D.2a3÷a=2a2 -
科目: 来源: 题型:
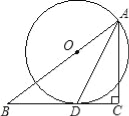
查看答案和解析>>【题目】如图,在△ABC中,∠C=90°,AD是∠BAC的平分线,O是AB上一点,以O为圆心,OA为半径的⊙O经过点D.
(1)求证:BC是⊙O的切线;
(2)若BD=5,DC=3,求AC的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,O为直线AB上一点,∠AOC=50°,OD平分∠AOC,∠DOE=90°
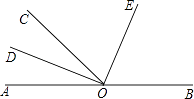
(1)请你数一数,图中有多少个小于平角的角;
(2)求出∠BOD的度数;
(3)请通过计算说明OE是否平分∠BOC. -
科目: 来源: 题型:
查看答案和解析>>【题目】若a>0,b<﹣2,则点(a,b+2)在( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
相关试题

