【题目】记M(1)=-2,M(2)=(-2)×(-2),M(3)=(-2)×(-2)×(-2),……![]()
(Ⅰ) 计算:M(5)+M(6);
(Ⅱ) 求2M(2015)+M(2016)的值:
(Ⅲ) 说明2M(n)与M(n+1)互为相反数.
参考答案:
【答案】(Ⅰ)根据题意,可知M(n)=(-2)n , 即可分别表示出M(5)和M(6) , 分别计算,然后求和,即可求解;
(Ⅱ)根据M(n)=(-2)n , 可分别表示出M(2015)和M(2016) , 根据2×(-2)2015=-(-2)2016 , 即可求解;
(Ⅲ)同理,分别表示出M(n)和M(n+1) , 根据2×(-2)n=-(-2)n+1 , 即可得解.
试题解析:(Ⅰ)∵M(n)=(-2) ×(-2) ×(-2)×. . . (n个-2相乘),即M(n)=(-2)n ,
∴M(5)+M(6)=(-2)5+(-2)6=-32+64=32;
(Ⅱ)∵M(n)=(-2)n ,
∴2M(2015)+M(2016)=2×(-2)2015+(-2)2016=-(-2)2016+(-2)2016=0;
(Ⅲ)∵M(n)=(-2)n ,
∴2M(n)+M(n+1)=2×(-2)n+(-2)n+1=-(-2)n+1+(-2)n+1=0,
∴2M(n)与M(n+1)互为相反数.
【解析】:同底数幂的乘法法则的使用条件是同底数幂相乘,即只要使底数相同的幂相乘就行,不论底数是单个的数字或字母,单项式还是多项式.同底数幂的乘法运算性质可以逆用,即一个幂可以写成两个同底数幂的积.
【考点精析】本题主要考查了同底数幂的乘法的相关知识点,需要掌握同底数幂的乘法法则aman=am+n(m,n都是正数)才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:∠MON=40°,OE平分∠MON,点A、B、C分别是射线OM、OE、ON上的动点(A、B、C不与点O重合),连接AC交射线OE于点D.设∠OAC=
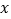 °.
°.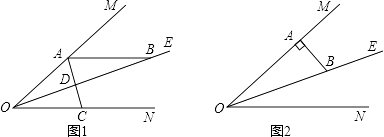
(1)如图1,若AB//ON,则①∠ABO的度数;②当∠BAD=∠ABD时,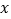 =;③当∠BAD=∠BDA时,
=;③当∠BAD=∠BDA时, 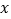 = .
= .
(2)如图2,若AB⊥OM,则是否存在这样的x的值,使得△ADB中有两个相等的角?若存在,求出x的值;若不存在,说明理由 . -
科目: 来源: 题型:
查看答案和解析>>【题目】“六一”儿童节前夕,薪黄县教育局准备给留守儿童赠送一批学习用品,先对浠泉镇浠泉小学的留守儿童人数进行抽样统计,发现各班留守儿童人数分别为6名,7名,8名,10名,12名这五种情形,并将统计结果绘制成了如图所示的两份不完整的统计图:
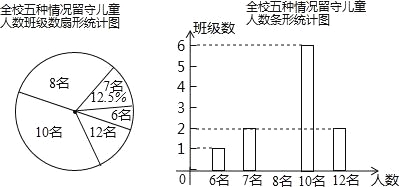
请根据上述统计图,解答下列问题:
(1)该校有多少个班级?并补充条形统计图;
(2)该校平均每班有多少名留守儿童?留守儿童人数的众数是多少?
(3)若该镇所有小学共有60个教学班,请根据样本数据,估计该镇小学生中,共有多少名留守儿童.
-
科目: 来源: 题型:
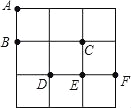
查看答案和解析>>【题目】在3×3的方格纸中,点A、B、C、D、E、F分别位于如图所示的小正方形的顶点上.
(1)从A、D、E、F四个点中任意取一点,以所取的这一点及点B、C为顶点画三角形,则所画三角形是等腰三角形的概率是 ;
(2)从A、D、E、F四个点中先后任意取两个不同的点,以所取的这两点及点B、C为顶点画四边形,求所画四边形是平行四边形的概率是 (用树状图或列表法求解).
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:a2a3= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列各数中,最小的数是( )
A.5
B.﹣3
C.0
D.2 -
科目: 来源: 题型:
查看答案和解析>>【题目】将直线y=2x-1向上平移2个单位得到的一次函数的关系式是:_______________.
相关试题

