【题目】如图,在⊙O中.

(1)若![]() ,∠ACB=70°,求∠BOC的度数;
,∠ACB=70°,求∠BOC的度数;
(2)若⊙O的半径为13,BC=10,求点O到BC的距离.
参考答案:
【答案】(1)证明见解析(2)12
【解析】试题分析:
(1)由已知条件可求得∠A的度数,再由圆周角定理可求得∠BOC的度数;
(2)过点O作OD⊥BC于点D,由垂径定理可得BD=5,再在Rt△ABD中,由勾股定理可求得OD的长,从而可得点O到BC的距离.
试题解析:
(1)∵![]() ,
,
∴AB=AC.
∴∠ABC=∠ACB=70°
∴在△ABC中,∠BAC=180°-∠ABC-∠ACB=40°
∴∠BOC=2∠BACA=80° .
(2)作OD⊥BC,垂足为点D
∵ OD⊥BC,OD过圆心
∴BD=![]() BC=5,
BC=5,
在Rt△BOD中:OD=![]() ,即点O到BC的距离为12.
,即点O到BC的距离为12.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC内接于⊙O,AB=AC,CO的延长线交AB于点D.
(1)求证:AO平分∠BAC;
(2)若BC=6,sin∠BAC=
 ,求AC和CD的长.
,求AC和CD的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(12分)如图,已知抛物线
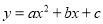 (
(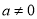 )的顶点坐标为(4,
)的顶点坐标为(4, 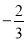 ),且与y轴交于点C(0,2),与x轴交于A、B两点(点A在点B的左边).
),且与y轴交于点C(0,2),与x轴交于A、B两点(点A在点B的左边).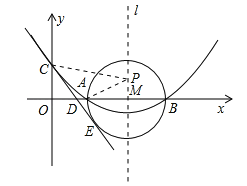
(1)求抛物线的解析式及A、B两点的坐标;
(2)在(1)中抛物线的对称轴l上是否存在一点P,使AP+CP的值最小,若存在,求AP+CP的最小值;若不存在,请说明理由;
(3)在以AB为直径的⊙M中,CE与⊙M相切于点E,CE交x轴于点D,求直线CE的解析式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列各组数是勾股数的是( )
A.2,3,4
B.4,5,6
C.3.6,4.8,6
D.9,40,41
-
科目: 来源: 题型:
查看答案和解析>>【题目】在某个变化过程中,有两个变量x与y,下列关系中一定能称y是x的函数的是( )
A. x=y2 B. y=x2+2x C. |y|=2x D. y2=2x+1
-
科目: 来源: 题型:
查看答案和解析>>【题目】点P(2017,﹣2018)在( )
A. 第一象限B. 第二象限C. 第三象限D. 第四象限
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列计算正确的是( )
A. aa2=a2B. (x3)2=x5
C. (2a)2=4a2D. (x+1)2=x2+1
相关试题

