【题目】如图1,已知矩形ABCD,E为AD边上一动点,过A,B,E三点作⊙O,P为AB的中点,连接OP, 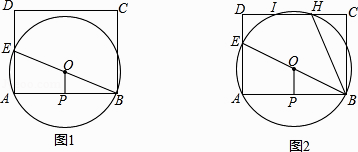
(1)求证:BE是⊙O的直径且OP⊥AB;
(2)若AB=BC=8,AE=6,试判断直线DC与⊙O的位置关系,并说明理由;
(3)如图2,若AB=10,BC=8,⊙O与DC边相交于H,I两点,连结BH,当∠ABE=∠CBH时,求△ABE的面积.
参考答案:
【答案】
(1)解:∵矩形ABCD,∴∠A=90°,∴BE为直径,
∴OE=OB,
∵AP=BP,
∴OP//AE,AE=2PO,
∴∠OPB=∠A=90°,
即OP⊥AB.
(2)解:此时直线CD与⊙O相切
理由:如图1,延长PO交CD于M,
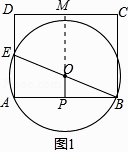
在Rt△ABE中,AB=8,AE=6,
则BE2=62+82=100,
∴BE=10,
∴此时⊙O的半径r=5,∴OM=r=5,
∵在矩形APMD中,PM=AD=8,
∴OM=PM﹣OP=5=r,
∴直线CD与⊙O相切
(3)解:【方法I】如图2,
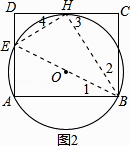
∵BE为直径,
∴∠EHB=90°,
∴∠3+∠4=90°,
∵∠C=90°,
∴∠3+∠2=90°,
∴∠2=∠4,
∴当∠1=∠2时,有
tan∠1=tan∠2=tan∠4,
设AE=x,CH=y,则DE=8﹣x,DH=10﹣y,
∴ ![]() =
= ![]() =
= ![]() ,
,
解得,x=20,或x=5,
∵AE=x<8,∴x=20,不合题意,舍去,取AE=x=5,
Rt△ABE的面积= ![]() AE×AB=
AE×AB= ![]() ×5×10=25.
×5×10=25.
【方法II】如图3,延长PO交CD于点F,连接OH,
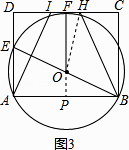
在矩形FPBC,OP⊥AB,且FC=PB= ![]() AB=5,
AB=5,
OP= ![]() AE,OF=8﹣
AE,OF=8﹣ ![]() AE,BE=2HO,
AE,BE=2HO,
当∠ABE=∠CBH时,设tan∠ABE=tan∠CBH=k时,
在Rt△ABE中,则AE=10tan∠ABE=10k,
在Rt△HBC中,则HC=8tan∠ABE=8k,
∴OP=5k,OF=8﹣5k,FH=5﹣8k,
在Rt△ABE中,BE2=AE2+AB2=100(1+k2),
在Rt△OFH中,HO2=FH2+OF2=(5﹣8k)2+(8﹣5k)2,
∵BE=2HO,∴BE2=4 HO2
∴100(1+k2)=4[(5﹣8k)2+(8﹣5k)2],
整理得,2 k2﹣5k+2=0,
解得,k=2,或k= ![]() ,
,
当k=2时,AE=10k=20>8,不合题意,舍去;
当k= ![]() 时,AE=10k=5<8,符合题意,
时,AE=10k=5<8,符合题意,
此时,Rt△ABE的面积= ![]() AE×AB=
AE×AB= ![]() ×5×10=25
×5×10=25
【解析】(1)利用矩形的性质以及平行线分线段成比例定理得出OP//AE,AE=2PO,即可得出答案;(2)首先延长PO交CD于M,求出MO的长等于半径,进而得出答案;(3)根据题意当∠1=∠2时,可得出tan∠1=tan∠2=tan∠4,设AE=x,CH=y,则DE=8﹣x,DH=10﹣y,可得 ![]() =
= ![]() =
= ![]() ,求出x的值,即可得出答案.
,求出x的值,即可得出答案.
-
科目: 来源: 题型:
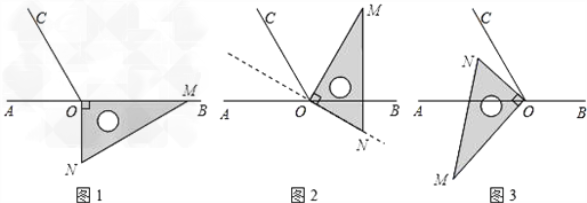
查看答案和解析>>【题目】如图1,点O为直线AB上一点,过点O作射线OC,使∠BOC=120°.将一直角三角板的直角顶点放在点O处,一边OM在射线OB上,另一边ON在直线AB的下方.
(1)将图1中的三角板绕点O逆时针旋转至图2,使一边OM在∠BOC的内部,且恰好平分∠BOC.问:此时直线ON是否平分∠AOC?请说明理由.
(2)将图1中的三角板绕点O以每秒6°的速度沿逆时针方向旋转一周,在旋转的过程中,第t秒时,直线ON恰好平分锐角∠AOC,则t的值为_________(直接写出结果).
(3)将图1中的三角板绕点O顺时针旋转至图3,使ON在∠AOC的内部,请探究:∠AOM与∠NOC之间的数量关系,并说明理由。
-
科目: 来源: 题型:
查看答案和解析>>【题目】将一列有理数﹣1,2,﹣3,4,﹣5,6,……,如图所示有序排列,根据图中的排列规律可知,“峰1”中峰顶的位置(C的位置)是有理数4,那么,“峰5”中C的位置是有理数___,﹣2019应排在A、B、C、D、E中的___位置.其中两个填空依次为( )
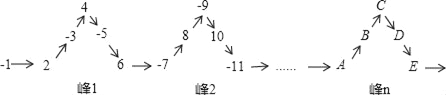
A. 24,C B. 24.A C. 25,B D. ﹣25,E
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点 O 是等边△ABC 内一点,∠AOB=105°,∠BOC 等于α,将△BOC 绕点 C 按 顺时针方向旋转 60°得△ADC,连接 OD.
(1)求证:△COD 是等边三角形.
(2)求∠OAD 的度数.
(3)探究:当α为多少度时,△AOD 是等腰三角形?

-
科目: 来源: 题型:
查看答案和解析>>【题目】“幸福是奋斗出来的”,在数轴上,若C到A的距离刚好是3,则C点叫做A的“幸福点”,若C到A、B的距离之和为6,则C叫做A、B的“幸福中心”
(1)如图1,点A表示的数为﹣1,则A的幸福点C所表示的数应该是 ;
(2)如图2,M、N为数轴上两点,点M所表示的数为4,点N所表示的数为﹣2,点C就是M、N的幸福中心,则C所表示的数可以是 (填一个即可);
(3)如图3,A、B、P为数轴上三点,点A所表示的数为﹣1,点B所表示的数为4,点P所表示的数为8,现有一只电子蚂蚁从点P出发,以2个单位每秒的速度向左运动,当经过多少秒时,电子蚂蚁是A和B的幸福中心?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,已知抛物线y=ax2+bx+3(a≠0)与x轴交于点A(1,0)和点B(﹣3,0),与y轴交于点C.

(1)求抛物线的解析式;
(2)设抛物线的对称轴与x轴交于点M,问在对称轴上是否存在点P,使△CMP为等腰三角形?若存在,请直接写出所有符合条件的点P的坐标;若不存在,请说明理由;
(3)如图②,若点E为第二象限抛物线上一动点,连接BE、CE,求四边形BOCE面积的最大值,并求此时E点的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列计算正确的是( )
A.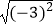 =﹣3
=﹣3
B.a2+a4=a6
C.(﹣ )﹣1=
)﹣1= 
D.(﹣π)0=1
相关试题

