【题目】如图,Rt△ABC中,M为斜边AB上一点,且MB=MC=AC=8cm,平行于BC的直线l从BC的位置出发以每秒1cm的速度向上平移,运动到经过点M时停止. 直线l分别交线段MB、MC、AC于点D、E、P,以DE为边向下作等边△DEF,设△DEF与△MBC重叠部分的面积为S(cm2),直线l的运动时间为t(秒).

(1)求边BC的长度;
(2)求S与t的函数关系式;
(3)在整个运动过程中,是否存在这样的时刻t,使得以P、C、F为顶点的三角形为等腰三角形?若存在,请求出t的值;若不存在,请说明理由.
(4)在整个运动过程中,是否存在这样的时刻t,使得以点D为圆心、BD为半径的圆与直线EF相切?若存在,请求出t的值;若不存在,请说明理由.
参考答案:
【答案】(1) 8![]() ;(2) 当0<t≤3时,S=﹣
;(2) 当0<t≤3时,S=﹣![]() t2+8
t2+8![]() t;当3<t≤4时,S= 3
t;当3<t≤4时,S= 3![]() t2﹣24
t2﹣24![]() t+48
t+48![]() .(3) t=
.(3) t=![]() (4) t=
(4) t=![]() .
.
【解析】
试题分析:(1)利用直角三角形的性质和锐角三角函数即可;
(2)分两段求出函数关系即可;
(3)进行分类讨论即可求出t的值;
(4)若相切,利用点到圆心的距离等于半径列出方程即可.
试题解析:(1)∵M为斜边中点,
∴∠B=MCB=α,
∴∠AMC=2α,
∵MC=MA,
∴∠A=∠AMC=2α,
∴∠B+∠A=90°,
∴α+2α=90°,
∴α=30°,
∴∠B=30°,
∵cotB=![]() ,
,
∴BC=AC×cotB=8![]() ;
;
(2)由题意,若点F恰好落在BC上,
∴MF=4(4﹣t)=4,
∴t=3.
当0<t≤3时,如图,
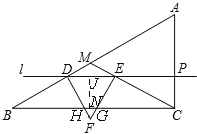
∴BD=2t,DM=8﹣2t,
∵l∥BC,
∴![]() ,
,
∴![]() ,
,
∴DE=![]() (8﹣2t).
(8﹣2t).
∴点D到EF的距离为FJ=![]() DE=3(4﹣t),
DE=3(4﹣t),
∵l∥BC,
∴![]() ,
,
∵FN=FJ﹣JN=3(4﹣t)﹣t=12﹣4t,
∴HG=![]() (3﹣t)
(3﹣t)
S=S梯形DHGE=![]() (HG+DE)×FN=﹣
(HG+DE)×FN=﹣![]() t2+8
t2+8![]() t
t
当3<t≤4时,重叠部分就是△DEF,
S=S△DEF=![]() DE2=3
DE2=3![]() t2﹣24
t2﹣24![]() t+48
t+48![]() .
.
(3)当0<t≤3时,∠FCP≥90°,
∴FC>CP,
∴△PCF不可能为等腰三角形
当3<t≤4时,若△PCF为等腰三角形,
∴只能FC=FP,
∴![]() =3(4﹣t),
=3(4﹣t),
∴t=![]()
(4)若相切,
∵∠B=30°,
∴BD=2t,DM=8﹣2t,
∵l∥BC,
∴![]() ,
,
∴![]() ,
,
∴DE=![]() (8﹣2t).
(8﹣2t).
∴点D到EF的距离为![]() DE=3(4﹣t)
DE=3(4﹣t)
∴2t=3(4﹣t),
解得t=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果一个等腰三角形的一个角等于80°,则底角的度数是 _______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某厂生产A、B两种产品,其单价随市场变化而做相应调整,营销人员根据前三次单价变化的情况,绘制了如下统计表及不完整的折线图.

并求得了A产品三次单价的平均数和方差:
A=5.9;s2A=[(6-5.9)2+(5.2-5.9)2+(6.5-5.9)2]= .
(1)补全图中B产品单价变化的折线图. B产品第三次的单价比上一次的单价降低了 %;
(2)求B产品三次单价的方差,并比较哪种产品的单价波动小;
(3)该厂决定第四次调价,A产品的单价仍为6.5元/件,B产品的单价比3元/件上调m%(m>0),使得A产品这四次单价的中位数是B产品四次单价中位数的2倍少1,求m的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】南海是我国的南大门,如图所示,某天我国一艘海监执法船在南海海域正在进行常态化巡航,在A处测得北偏东30°方向上,距离为20海里的B处有一艘不明身份的船只正在向正东方向航行,便迅速沿北偏东75°的方向前往监视巡查,经过一段时间后,在C处成功拦截不明船只,问我海监执法船在前往监视巡查的过程中行驶了多少海里(最后结果保留整数)?
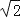
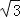 (参考数据:cos75°=0.2588,sin75°=0.9659,tan75°=3.732,
(参考数据:cos75°=0.2588,sin75°=0.9659,tan75°=3.732, =1.732,
=1.732, =1.414)
=1.414)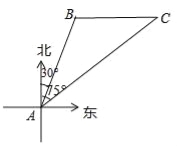
-
科目: 来源: 题型:
查看答案和解析>>【题目】据统计,2017年端午小长假全国各大景点共接待游客约为82600000人次,将82600000用科学记数法表示为( )
A. 0.826×106 B. 8.26×108 C. 8.26×107 D. 82.6×106
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法正确的是 ( )
A. x的次数是0 B. x的系数是0 C. -1是一次单项式 D. -1是零次单项式
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知a﹣b=3,那么1﹣a+b=( )
A. ﹣2 B. 4 C. 1 D. ﹣1
相关试题

