【题目】在△ABC中，点P是平面内任意一点（不同于A、B、C），若点P与A、B、C中的某两点的连线的夹角为直角时，则称点P为△ABC的一个勾股点.

（1）如图1，若点P是△ABC内一点，∠A=55°，∠ABP=10°，∠ACP=25°，试说明点P是△ABC的一个勾股点；

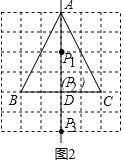
（2）如图2，等腰△ABC的顶点都在格点上，点D是BC的中点，点P在直线AD上，请在图中标出使得点P是△ABC的勾股点时，点P的位置；

（3）在Rt△ABC中，∠ACB=90°，AC=12，BC=16，点D是AB的中点，点P在射线CD上.若点P是△ABC的勾股点，请求出CP的长；

参考答案：

【答案】（1）见解析；(2)见解析；(3)7.2或12.8或20．

【解析】

（1）根据三角形内角和定理，证得∠CPB＝90°即可；

（2）根据网格特点以及勾股点的定义进行解答即可；

（3）分情况讨论：①∠APC＝90°时．②当∠CPB＝90°时．③当∠APB＝90°时．分别求解即可．

解：（1）在△ABC中，∠A＝55°，

∴∠ACB+∠ABC＝125°．

∵∠ACP＝10°，∠ABP＝25°，

∴∠PCB+∠PBC＝90°．

∴∠CPB＝90°，

∴点P是△ABC的一个勾股点．

（2）如图，点P1，P2，P3即为所求．

（3）在Rt△ABC中，∠ACB＝90°，AC＝12，BC＝16．

∴AB＝20，

又∵点D是AB的中点，

∴AD＝BD＝CD＝10，

①∠APC＝90°时，设CP＝x，DP＝10﹣x，

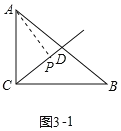
在Rt△APC和Rt△APD中，

∵AC2﹣CP2＝AD2﹣DP2，即：122﹣x2＝102﹣（10﹣x）2，

解得：x＝7.2．

②当∠CPB＝90°时，设CP＝x，DP＝x﹣10，

在Rt△BPD和Rt△BPC中，∵BC2﹣CP2＝BD2﹣DP2，即162﹣x2＝102﹣（x﹣10）2，

解得：x＝12.8．

③当∠APB＝90°时，

在Rt△APB中，DP＝AB＝10，

∴CP＝20

综上所述，CP的长为7.2或12.8或20．

关闭