【题目】已知等边△ABC中,点D为射线BA上一点,作DE=DC,交直线BC于点E,∠ABC的平分线BF交CD于点F,过点A作AH⊥CD于H,当EDC=30![]() ,CF=
,CF=![]() ,则DH=______.
,则DH=______.

参考答案:
【答案】![]()
【解析】连接AF.
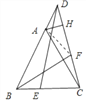
∵△ABC是等边三角形,
∴AB=BC,∠ABC=∠ACB=∠BAC=60°.
∵DE=DC,∠EDC=30°,
∴∠DEC=∠DCE=75°,
∴∠ACF=75°-60°=15°.
∵BF平分∠ABC,
∴∠ABF=∠CBF.
在△ABF和△CBF中, 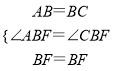 ,
,
∴△ABF≌△CBF,
∴AF=CF,
∴∠FAC=∠ACF=15°,
∴∠AFH=15°+15°=30°.
∵AH⊥CD,
∴AH=![]() AF=
AF=![]() CF=
CF=![]() .
.
∵∠DEC=∠ABC+∠BDE,
∴∠BDE=75°-60°=15°,
∴∠ADH=15°+30°=45°,
∴∠DAH=∠ADH=45°,
∴DH=AH=![]() .
.
故答案为: ![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读材料:
我们经常通过认识一个事物的局部或其特殊类型,来逐步认识这个事物;比如我们通过学习特殊的四边形,即平行四边形(继续学习它们的特殊类型如矩形、菱形等)来逐步认识四边形;

我们对课本里特殊四边形的学习,一般先学习图形的定义,再探索发现其性质和判定方法,然后通过解决简单的问题巩固所学知识;
请解决以下问题:
如图,我们把满足AB=AD、CB=CD且AB≠BC的四边形ABCD叫做“筝形”;
⑴写出筝形的两个性质(定义除外);
⑵写出筝形的两个判定方法(定义除外),并选出一个进行证明.

-
科目: 来源: 题型:
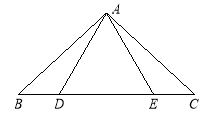
查看答案和解析>>【题目】如图,点D,E在△ABC的边BC上,连 接AD,AE.①AB=AC;②AD=AE;③BD=CE.以此三个等式中的两个作为命题的题设,另一个作为命题的结论,构成三个命题:①②③:①③②;②③①.
(1)以上三个命题是真命题的为(直接作答) ;
(2)请选择一个真命题进行证明(先写出所选命题,然后证明)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果点P(m+3,m﹣2)在x轴上,那么m=_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列计算正确的是( )
A.3a+2b=5abB.2a3+3a2=5a5C.3a2b-3ba2=0D.5a2-4a2=1
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列几种形状的瓷砖中,只用一种不能够铺满地面的是( )
A.正六边形
B.正五边形
C.正方形
D.正三角形 -
科目: 来源: 题型:
查看答案和解析>>【题目】把一些图书分给某班学生阅读,如果每人分3本,则剩余24本;如果每人分4本,则还缺26本.这个班有学生( )
A.40名B.55名C.50名D.60名
相关试题

