【题目】如图，正方形和，，，连接，．若绕点旋转，当最大时，__________．

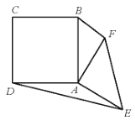
【答案】24

【解析】

作DH⊥AE于H，如图，由于AF=8，则△AEF绕点A旋转时，点F在以A为圆心，8为半径的圆上，当BF为此圆的切线时，∠ABF最大，即BF⊥AF，利用勾股定理计算出BF=6，接着证明△ADH≌△ABF得到DH=BF=6，然后根据三角形面积公式求解．

作DH⊥AE于H，如图，


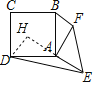
∵AF=8，当△AEF绕点A旋转时，点F在以A为圆心，8为半径的圆上，
∴当BF为此圆的切线时，∠ABF最大，即BF⊥AF，
在Rt△ABF中，BF= =6，
∵∠EAF=90°，
∴∠BAF+∠BAH=90°，
∵∠DAH+∠BAH=90°，
∴∠DAH=∠BAF，
在△ADH和△ABF中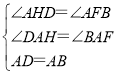
，
∴△ADH≌△ABF（AAS），
∴DH=BF=6，
∴S△ADE=AEDH=×6×8=24．
故答案为24．

关闭