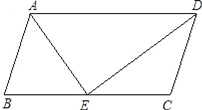
【题目】如图,已知平行四边形ABCD,DE是∠ADC的角平分线,交BC于点E.
(1)求证:CD=CE;
(2)若BE=CE,∠B=80°,求∠DAE的度数.
参考答案:
【答案】(1)证明见解析;(2)∠DAE=50°.
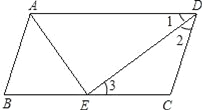
【解析】试题分析:(1)根据DE是∠ADC的角平分线得到∠1=∠2,再根据平行四边形的性质得到∠1=∠3,所以∠2=∠3,根据等角对等边即可得证;
(2)先根据BE=CE结合CD=CE得到△ABE是等腰三角形,求出∠BAE的度数,再根据平行四边形邻角互补得到∠BAD=100°,所以∠DAE可求.
(1)证明:如图,在平行四边形ABCD中,
∵AD∥BC
∴∠1=∠3
又∵∠1=∠2,
∴∠2=∠3,
∴CD=CE;
(2)解:∵四边形ABCD是平行四边形,
∴AB=CD,AD∥BC,
又∵CD=CE,BE=CE,
∴AB=BE,
∴∠BAE=∠BEA.
∵∠B=80°,
∴∠BAE=50°,
∴∠DAE=180°﹣50°﹣80°=50°.
点睛:本题主要考查平行四边形的性质,根据平行四边形的性质中对边平行,以及DE是∠ADC的平分线,证明△DEC是等腰三角形,以类似的方法也可以求出∠DAE的角度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中,AB>BC,按以下步骤作图:以A为圆心,小于AD的长为半径画弧,分别交AB、CD于E、F;再分别以E、F为圆心,大于
 EF的长半径画弧,两弧交于点G;作射线AG交CD于点H.则下列结论:①AG平分∠DAB,②CH=
EF的长半径画弧,两弧交于点G;作射线AG交CD于点H.则下列结论:①AG平分∠DAB,②CH= DH,③△ADH是等腰三角形,④S△ADH=
DH,③△ADH是等腰三角形,④S△ADH= S四边形ABCH.
S四边形ABCH.其中正确的有( )

A. ①②③ B. ①③④ C. ②④ D. ①③
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在梯形ABCD中,已知AD∥BC,∠B=90°,AB=7,AD=9,BC=12,在线段BC上任取一点E,连接DE,作EF⊥DE,交直线AB于点F.
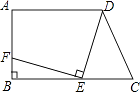
(1)若点F与B重合,求CE的长;
(2)若点F在线段AB上,且AF=CE,求CE的长;
(3)设CE=x,BF=y,写出y关于x的函数关系式(直接写出结果可). -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中,分别以AB、AD为边向外作等边△ABE、△ADF,延长CB交AE于点G,点G在点A、E之间,连接CE、CF,EF,则以下四个结论一定正确的是:①△CDF≌△EBC;②∠CDF=∠EAF;③△ECF是等边△;④CG⊥AE( )
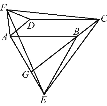
A. 只有①② B. 只有①②③ C. 只有③④ D. ①②③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一次机器人测试中,要求机器人从A出发到达B处.如图1,已知点A在O的正西方600cm处,B在O的正北方300cm处,且机器人在射线AO及其右侧(AO下方)区域的速度为20cm/秒,在射线AO的左侧(AO上方)区域的速度为10cm/秒.
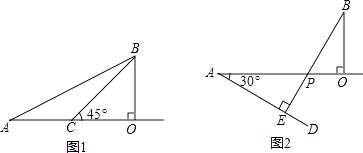
(参考数据: ≈1.414,
≈1.414,  ≈1.732,
≈1.732,  ≈2.236,
≈2.236, 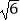 ≈2.449)
≈2.449)
(1)分别求机器人沿A→O→B路线和沿A→B路线到达B处所用的时间(精确到秒);
(2)若∠OCB=45°,求机器人沿A→C→B路线到达B处所用的时间(精确到秒);
(3)如图2,作∠OAD=30°,再作BE⊥AD于E,交OA于P.试说明:从A出发到达B处,机器人沿A→P→B路线行进所用时间最短. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平行四边形ABCD中,E是AD上一点,AE=AB,过点E作直线EF,在EF上取一点G,使得∠EGB=∠EAB,连接AG.
(1)如图①,当EF与AB相交时,若∠EAB=60°,求证:EG=AG+BG;
(2)如图②,当EF与CD相交时,且∠EAB=90°,请你写出线段EG、AG、BG之间的数量关系,并证明你的结论.

-
科目: 来源: 题型:
查看答案和解析>>【题目】同庆中学为丰富学生的校园生活,准备从军跃体育用品商店一次性购买若干个足球和篮球(每个足球的价格相同,每个篮球的价格相同),若购买3个足球和2个篮球共需310元,购买2个足球和5个篮球共需500元.
(1)购买一个足球、一个篮球各需多少元?
(2)根据同庆中学的实际情况,需从军跃体育用品商店一次性购买足球和篮球共96个,要求购买足球和篮球的总费用不超过5720元,这所中学最多可以购买多少个篮球?
相关试题

