【题目】如图,△ABC中,∠C=90°,AB=10cm,BC=6cm,若动点P从点C开始,按C→A→B→C
的路径运动,且速度为每秒1cm,设出发的时间为t秒.
(1)出发2秒后,求△ABP的周长.
(2)当t为几秒时,BP平分∠ABC
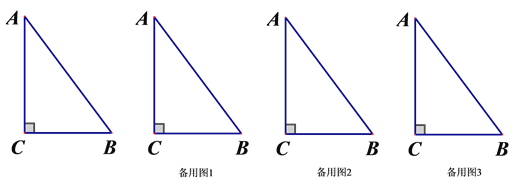
(3)问t为何值时,△BCP为等腰三角形?
参考答案:
【答案】(1)16+2![]() ;(2)3;(3)6s或13s或12s或 10.8s.
;(2)3;(3)6s或13s或12s或 10.8s.
【解析】分析:(1)利用勾股定理得出AC=8cm,进而表示出AP的长,由勾股定理求出PB,进而得出答案;(2)过点P作PD⊥AB于点D,由HL证明Rt△BPD≌Rt△BPC,得出BD=BC=6cm,因此BD=10-6=4cm,设PC=x cm,则PA=(8-x)cm,由勾股定理得出方程,解方程即可;(3)利用分类讨论的思想和等腰三角形的特点及三角形的面积求出答案.
本题解析:
(1)∵∠C=90,AB=10cm,BC=6cm,∴有勾股定理得AC=8cm,动点P从点C开始,按![]() 的路径运动,且速度为每秒1cm
的路径运动,且速度为每秒1cm
∴出发2秒后,则CP=2cm,那么AP=6cm.
∵∠C=90°,
∴由勾股定理得PB=2![]() cm
cm
∴△ABP的周长为:AP+PB+AB=6+10+2![]() =(16+2
=(16+2![]() )cm;
)cm;
(2)如图2所示,过点P作PD⊥AB于点D,

∵BP平分∠ABC,∴PD=PC.
在Rt△BPD与Rt△BPC中, ![]() ,
,
∴Rt△BPD≌Rt△BPC(HL),
∴BD=BC=6 cm,
∴AD=106=4 cm.
设PC=x cm,则PA=(8x)cm
在Rt△APD中,PD+AD=PA,
即x+4=(8x),
解得:x=3,
∴当t=3秒时,AP平分∠CAB;
(3)若P在边AC上时,BC=CP=6cm,
此时用的时间为6s,△BCP为等腰三角形;
若P在AB边上时,有两种情况:
①若使BP=CB=6cm,此时AP=4cm,P运动的路程为12cm,
所以用的时间为12s,故t=12s时△BCP为等腰三角形;
②若CP=BC=6cm,过C作斜边AB的高,根据面积法求得高为4.8cm,
根据勾股定理求得BP=7.2cm,
所以P运动的路程为187.2=10.8cm,
∴t的时间为10.8s,△BCP为等腰三角形;
③若BP=CP时,则∠PCB=∠PBC,
∵∠ACP+∠BCP=90°,∠PBC+∠CAP=90°,∴∠ACP=∠CAP,∴PA=PC
∴PA=PB=5cm
∴P的路程为13cm,所以时间为13s时,△BCP为等腰三角形。
∴t=6s或13s或12s或 10.8s 时△BCP为等腰三角形。
-
科目: 来源: 题型:
查看答案和解析>>【题目】 将点M(-5,y)向上平移6个单位长度后得到的点与点M关于x轴对称,则y的值是( )
A.-6B.6C.-3D.3
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线y=kx+b,若k+b=5,kb=6,那么该直线不经过第__象限.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题中正确的是( )
A. 有一组邻边相等的四边形是菱形B. 有一个角是直角的四边形是矩形
C. 对角线互相垂直的平行四边形是正方形D. 对角线互相平分的四边形是平行四边形
-
科目: 来源: 题型:
查看答案和解析>>【题目】观察下列有规律的数:
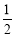 ,
,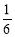 ,
,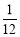 ,
,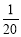 ,
,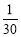 ,
,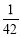 ……根据规律可知,
……根据规律可知,(1)第7个数_____________,第n个数是______________(n是正整数).
(2)
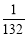 是第__________个数.
是第__________个数.(3)计算
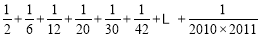 .(本题6分)
.(本题6分) -
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的二次函数y=ax2+bx+c的图象经过点(﹣2,y1),(﹣1,y2),(1,0),且y1<0<y2,对于以下结论:①abc>0;②a+3b+2c≤0;③对于自变量x的任意一个取值,都有
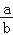 x2+x≥﹣
x2+x≥﹣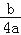 ;④在﹣2<x<﹣1中存在一个实数x0,使得x0=﹣
;④在﹣2<x<﹣1中存在一个实数x0,使得x0=﹣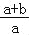 ,其中结论错误的是 (只填写序号).
,其中结论错误的是 (只填写序号). -
科目: 来源: 题型:
查看答案和解析>>【题目】一人驾驶快船沿江顺流而下,迎面遇到一艘逆流而上的快艇.他问快艇驾驶员:“你后面有轮船开过吗”快艇驾驶员回答:“半小时前我超过一艘轮船”.快船继续航行了半小时,遇到了迎面而来的轮船.已知轮船静水速度是快船静水速度的2倍,那么快艇静水速度是快船的静水速度的____倍.
相关试题

