【题目】如图,在菱形ABCD中,对角线AC、BD交于点O,以OB为直径画圆M,过D作⊙M的切线,切点为N,分别交AC、BC于点E、F,已知AE=5,CE=3,则菱形ABCD的面积是( )
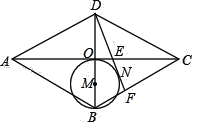
A. 24B. 20C. ![]() D.
D. ![]()
参考答案:
【答案】D
【解析】
连接MN,根据题意可得OE=1,因为DN为⊙M的切线,所以EN=EO=1,易证△DEO∽△DMN,且MN=![]() DM,则DE=3OE=3,在Rt△DMN中,利用勾股定理即可求得MN的长,即可得BD的长,再利用菱形的面积公式求解即可.
DM,则DE=3OE=3,在Rt△DMN中,利用勾股定理即可求得MN的长,即可得BD的长,再利用菱形的面积公式求解即可.
解:如图,连接MN,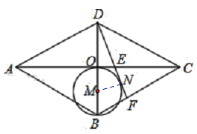
∵AE=5,CE=3,DN为⊙M的切线,
∴OE=EN=1,
易证△DEO∽△DMN,且MN=![]() DM,
DM,
则DE=3OE=3,
在Rt△DMN中,MN2+DN2=DM2,即MN2+16=9 MN2,
解得MN=![]() ,则BD=4MN=4
,则BD=4MN=4![]() ,
,
则菱形ABCD的面积=![]() BD·AC=
BD·AC=![]() .
.
故选D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】“一带一路”的战略构想为国内许多企业的发展带来了新的机遇,某公司生产A,B两种机械设备,每台B种设备的成本是A种设备的1.5倍,公司若投入16万元生产A种设备,36万元生产B种设备,则可生产两种设备共10台.请解答下列问题:
(1)A、B两种设备每台的成本分别是多少万元?
(2)若A,B两种设备每台的售价分别是6万元,10万元,公司决定生产两种设备共60台,计划销售后获利不低于126万元,且A种设备至少生产53台,求该公司有几种生产方案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图1,等边△ABC内接于⊙O,点P是⌒AB上的任意一点,连结PA,PB,PC.点D是PC上一点,连结DB.
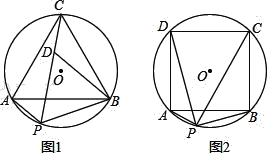
(1) 若PD=PB,求∠PBD的度数;
(2)在(1)的条件下,小丽探究
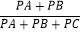 的值,她认为只要弄清PA+PB与PC的关系即可,她的思路可以用以下框图表示:
的值,她认为只要弄清PA+PB与PC的关系即可,她的思路可以用以下框图表示:
根据小丽的思路,请你完整地书写本题的探究过程,并求出
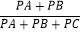 的值.
的值.(3)如图2,把条件“等边△ABC”改为“正方形ABCD”,其余条件不变,判断
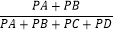 是定值吗?若是,请求出这个值;若不是,请说明理由.
是定值吗?若是,请求出这个值;若不是,请说明理由. -
科目: 来源: 题型:
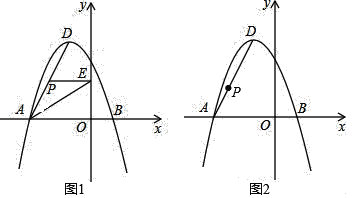
查看答案和解析>>【题目】如图,在平面直角坐标系中,抛物线y=ax2+bx+3经过A(﹣3,0)、B(1,0)两点,其顶点为D,连接AD,点P是线段AD上一个动点(不与A、D重合).
(1)求抛物线的函数解析式,并写出顶点D的坐标;
(2)如图1,过点P作PE⊥y轴于点E.求△PAE面积S的最大值;
(3)如图2,抛物线上是否存在一点Q,使得四边形OAPQ为平行四边形?若存在求出Q点坐标,若不存在请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知G是直角三角形ABC的内心,∠C=90°,AC=6,BC=8,则线段CG的长为______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在反比例函数图象中,△AOB是等边三角形,点A在双曲线的一支上,将△AOB绕点O顺时针旋转α (0°<α<360° ),使点A仍在双曲线上,则α=_____.
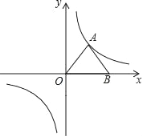
-
科目: 来源: 题型:
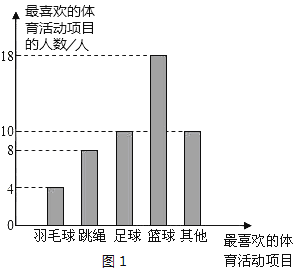
查看答案和解析>>【题目】某校围绕着“你最喜欢的体育活动项目是什么?(只写一项)”的问题,对在校学生进行了随机抽样调查,从而得到一组数据,如图1是根据这组数据绘制的条形统计图,请结合统计图回答下列问题:
(1)该校对多少名学生进行了抽样调查?
(2)本次抽样调查中,最喜欢足球活动的有多少人?占被调查人数的百分比是多少?
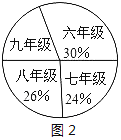
(3)若该校九年级共有400名学生,图2是根据各年级学生人数占全校学生总人数的百分比绘制的扇形统计图,请你估计全校学生中最喜欢篮球活动的人数约为多少?
相关试题

