【题目】如图,在正方形网格中,每个小正方形的边长都为1,网格中有一个格点△ABC(即三角形的顶点都在格点上).
(1)△ABC的面积为__________;
(2)在图中作出△ABC关于直线MN的对称图形△A′B′C′.
(3)利用网格纸,在MN上找一点P,使得PB+PC的距离最短.( 保留痕迹)

参考答案:
【答案】(1)4;(2)见解析;(3)见解析.
【解析】试题分析:(1)利用矩形的面积减去三个顶点上三角形的面积即可;
(2)分别作出各点关于直线MN的对称点,再顺次连接即可;
(3)连接BC′交直线MN于点P,则点P即为所求点.
试题解析:
(1)S△ABC=3×4-![]() ×2×2-
×2×2-![]() ×1×4-
×1×4-![]() ×2×3=12-2-3-3=4.
×2×3=12-2-3-3=4.
故答案为:4;
(2)如图,△A′B′C′即为所求;
(3)如图,点P即为所求.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABF中,以AB为直径的圆分别交边AF、BF于C、E两点,CD⊥AF.AC是∠DAB的平分线,

(1)求证:直线CD是⊙O的切线.
(2)求证:△FEC是等腰三角形. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,DM垂直平分AC,交BC于点D,连接AD,若∠C=28°,AB=BD,则∠B的度数为_____度.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在△ABC中,∠BAC=106°,EF、MN分别是AB、AC的垂直平分线,点E、M在BC上,则∠EAN=_____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读资料:我们把顶点在圆上,并且一边和圆相交、另一边和圆相切的角叫做弦切角,如图1∠ABC所示.同学们研究发现:P为圆上任意一点,当弦AC经过圆心O时,且AB切⊙O于点A,此时弦切角∠CAB=∠P(图2)
证明:∵AB切⊙O于点A,∴∠CAB=90°,又∵AC是直径,∴∠P=90°∴∠CAB=∠P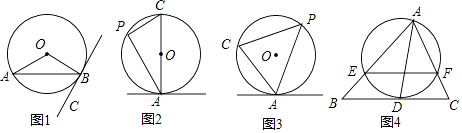
问题拓展:若AC不经过圆心O(如图3),该结论:弦切角∠CAB=∠P还成立吗?请说明理由.
知识运用:如图4,AD是△ABC中∠BAC的平分线,经过点A的⊙O与BC切于点D,与AB、AC分别相交于E、F.求证:EF∥BC. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,反比例函数y=
 (x>0)的图象经过点A(2
(x>0)的图象经过点A(2  ,1),射线AB与反比例函数图象交与另一点B(1,a),射线AC与y轴交于点C,∠BAC=75°,AD⊥y轴,垂足为D.
,1),射线AB与反比例函数图象交与另一点B(1,a),射线AC与y轴交于点C,∠BAC=75°,AD⊥y轴,垂足为D.
(1)求k和a的值;
(2)直线AC的解析式;
(3)如图3,M是线段AC上方反比例函数图象上一动点,过M作直线l⊥x轴,与AC相交于N,连接CM,求△CMN面积的最大值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将△ABC绕着点C顺时针旋转50°后得到△A′B′C′.若∠A=40°.∠B′=110°,则∠BCA′的度数是( )

A.110°
B.80°
C.40°
D.30°
相关试题

