搜索
【题目】若△ABC中，∠A∶∠B∶∠C＝1∶2∶3，则△ABC一定是( )
A. 锐角三角形 B. 钝角三角形 C. 直角三角形 D. 等腰三角形
参考答案：
【答案】C
【解析】解：∵△ABC中，∠A：∠B：∠C=1：2：3，∴设∠A=x°，∠B=2x°，∠C=3x°，∵∠A+∠B+∠C=180，∴x+2x+3x=180°，∴x=30，∴∠C=90°，∠A=30°，∠B=60°，即△ABC是直角三角形，故选C．
-
科目： 来源： 题型：
查看答案和解析>>【题目】抛物线y=2（x﹣3）2+1的顶点坐标是（ ）
A.（3，1）
B.（3，﹣1）
C.（﹣3，1）
D.（﹣3，﹣1） -
科目： 来源： 题型：
查看答案和解析>>【题目】已知任意三角形的三边长，如何求三角形面积？
古希腊的几何学家海伦解决了这个问题，在他的著作《度量论》一书中给出了计算公式﹣﹣海伦公式S=
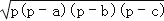（其中a，b，c是三角形的三边长，p=
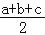，S为三角形的面积），并给出了证明例如：在△ABC中，a=3，b=4，c=5，那么它的面积可以这样计算：
∵a=3，b=4，c=5
∴p=
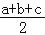=6∴S=
=
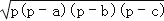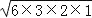=6事实上，对于已知三角形的三边长求三角形面积的问题，还可用我国南宋时期数学家秦九韶提出的秦九韶公式等方法解决．
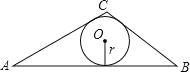
如图，在△ABC中，BC=5，AC=6，AB=9
（1）用海伦公式求△ABC的面积；
（2）求△ABC的内切圆半径r．
-
科目： 来源： 题型：
查看答案和解析>>【题目】若等腰三角形的两边长为6，8，则它的周长是 ．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，△ABC中，∠ACB=90°，AC=6cm，BC=8cm．点P从A点出发沿A→C→B路径向终点运动，终点为B点；点Q从B点出发沿B→C→A路径向终点运动，终点为A点．点P和Q分别以每秒1cm和3cm的运动速度同时开始运动，两点都要到相应的终点时才能停止运动，在某时刻，分别过P和Q作PE⊥l于E，QF⊥l于F．设运动时间为t秒，则当t=_________秒时，△PEC与△QFC全等．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，△ABC中，AB=AC，∠BAC=54°，点D为AB中点，且OD⊥AB，∠BAC的平分线与AB的垂直平分线交于点O，将∠C沿EF（E在BC上，F在AC上）折叠，点C与点O恰好重合，则∠OEC为______ °
-
科目： 来源： 题型：
查看答案和解析>>【题目】一个两位数是a，还有一个三位数是b，如果把这个两位数放在这个三位数的前面，组成一个五位数，则这个五位数的表示方法是（ ）
A. 10a+b B. 100a+b C. 1000a+b D. a+b
相关试题
