【题目】如图,△OAC和△BAD都是等腰直角三角形,∠ACO=∠ADB=90°,反比例函数![]() 在第一象限的图象经过点B,则△OAC与△BAD的面积之差S△OAC﹣S△BAD为( )
在第一象限的图象经过点B,则△OAC与△BAD的面积之差S△OAC﹣S△BAD为( )

A. 36 B. 12 C. 6 D. 3
参考答案:
【答案】D
【解析】设△OAC和△BAD的直角边长分别为a、b,结合等腰直角三角形的性质及图象可得出点B的坐标,根据三角形的面积公式结合反比例函数系数k的几何意义以及点B的坐标即可得出结论.
解:设△OAC和△BAD的直角边长分别为a、b,
则点B的坐标为(a+b,a﹣b).
∵点B在反比例函数![]() 的第一象限图象上,
的第一象限图象上,
∴(a+b)×(a﹣b)=a2﹣b2=6.
∴S△OAC﹣S△BAD=![]() a2﹣
a2﹣![]() b2=
b2=![]() (a2﹣b2)=
(a2﹣b2)=![]() ×6=3.
×6=3.
故选D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,⊙O的直径AB为4,C为⊙O上一个定点,∠ABC=30°,动点P从A点出发沿半圆弧
 向B点运动(点P与点C在直径AB的异侧),当P点到达B点时运动停止,在运动过程中,过点C作CP的垂线CD交PB的延长线于D点.
向B点运动(点P与点C在直径AB的异侧),当P点到达B点时运动停止,在运动过程中,过点C作CP的垂线CD交PB的延长线于D点.(1)求证:△ABC∽△PDC
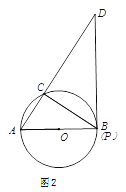
(2)如图2,当点P到达B点时,求CD的长;
(3)设CD的长为
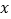 .在点P的运动过程中,
.在点P的运动过程中,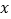 的取值范围为 (请直接写出答案).
的取值范围为 (请直接写出答案).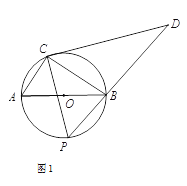
-
科目: 来源: 题型:
查看答案和解析>>【题目】“日落西山”是我们每天都要面对的自然变换,就你的理解,____是自变量,____是因变量.
-
科目: 来源: 题型:
查看答案和解析>>【题目】按字母x的升幂排列:x2-2y2+3xy .
-
科目: 来源: 题型:
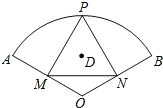
查看答案和解析>>【题目】如图,扇形OAB的圆心角的度数为120°,半径长为4,P为弧AB上的动点,PM⊥OA,PN⊥OB,垂足分别为M、N,D是△PMN的外心.当点P运动的过程中,点M、N分别在半径上作相应运动,从点N离开点O时起,到点M到达点O时止,点D运动的路径长 ( )
A.
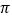 B.
B. 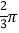 C. 2 D.
C. 2 D. 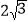
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算(-2x2)3的结果是( )
A. -2x5 B. -8x6 C. -2x6 D. -8x5
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列多项式,能用完全平方公式分解因式的是( )
A. -x2-2x-1 B. x2-2x-1 C. x2+xy+y2 D. x2+4
相关试题

