【题目】如图,已知数轴上点A表示的数为8,B是数轴上一点,且AB=14.动点P从点A出发,以每秒5个单位长度的速度沿数轴向左匀速运动,设运动时间为t(t>0)秒.
![]()
(1)写出数轴上点B表示的数 ,点P表示的数 (用含t的代数式表示);
(2)动点Q从点B出发,以每秒3个单位长度的速度沿数轴向左匀速运动,若点P、Q同时出发,问点P运动多少秒时追上点Q?
(3)若M为AP的中点,N为PB的中点.点P在运动的过程中,线段MN的长度是否发生变化?若变化,请说明理由;若不变,请你画出图形,并求出线段MN的长.
参考答案:
【答案】-6,8-5t;7秒;MN=7.
【解析】
试题分析:根据已知可得B点表示的数为8﹣14;点P表示的数为8﹣5t;点P运动x秒时,在点C处追上点Q,则AC=5x,BC=3x,根据AC﹣BC=AB,列出方程求解即可;分①当点P在点A、B两点之间运动时,②当点P运动到点B的左侧时,利用中点的定义和线段的和差求出MN的长即可
试题解析:(1)、∵点A表示的数为8,B在A点左边,AB=14, ∴点B表示的数是8﹣14=﹣6,
∵动点P从点A出发,以每秒5个单位长度的速度沿数轴向左匀速运动,设运动时间为t(t>0)秒,
∴点P表示的数是8﹣5t.
(2)、设点P运动x秒时,在点C处追上点Q,
![]()
则AC=5x,BC=3x, ∵AC﹣BC=AB, ∴5x﹣3x=14, 解得:x=7,
∴点P运动7秒时追上点Q.
(3)、线段MN的长度不发生变化,都等于7;理由如下:
∵①当点P在点A、B两点之间运动时:
![]()
MN=MP+NP=![]() AP+
AP+![]() BP=
BP=![]() (AP+BP)=
(AP+BP)=![]() AB=
AB=![]() ×14=7,
×14=7,
②当点P运动到点B的左侧时:
![]()
MN=MP﹣NP=![]() AP﹣
AP﹣![]() BP=
BP=![]() (AP﹣BP)=
(AP﹣BP)=![]() AB=7,
AB=7,
∴线段MN的长度不发生变化,其值为7.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题中,是假命题的是( )
A.两直线平行,内错角相等
B.同旁内角互补,两直线平行
C.无理数是无限循环小数
D.有限小数是有理数
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AC=BC,∠C=90°,点D是AB的中点.
(1)如图1,若点E、F分别是AC、BC上的点,且AE=CF,请判别△DEF的形状,并说明理由;
(2)若点E、F分别是CA、BC延长线上的点,且AE=CF,则(1)中的结论是否仍然成立?请
说明理由.
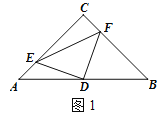
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市2019年10月底人口达到277.99万人,这个数据精确到( )
A.百分位B.百位C.千位D.万位
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,甲、乙两个容器内都装了一定数量的水,现将甲容器中的水匀速倒入乙容器中. 图2中,线段AB、线段CD分别表示容器中的水的深度h(厘米)与倒入时间t(分钟)的函数图像.
(1)请说出点C的纵坐标的实际意义;
(2)经过多长时间,甲、乙两个容器中的水的深度相等?
(3)如果甲容器的底面积为10cm2,求乙容器的底面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中, △ABC三个顶点的位置如图(每个小正方形的边长均为1).

(1)请画出△ABC沿x轴向右平移3个单位长度,再沿y轴向上平移2个单位长度后的△A′B′C′(其中A′、B′、C′分别是A、B、C的对应点,不写画法)
(2)直接写出A′、B′、C′三点的坐标:
A′(___________); B′(___________);C′(___________)。
(3)求△ABC的面积。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图, ⊙O 的半径是2,直线l与⊙O 相交于A、B 两点,M、N 是⊙O 上的两个动点,且在直线l的异侧,若∠AMB=45°,则四边形MANB 面积的最大值是 .

相关试题

