【题目】在△ABC中,MP,NO分别垂直平分AB,AC.
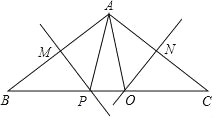
(1)若BC=1Ocm,试求出△PAO的周长.(不用写过程,直接写出答案)
(2)若AB=AC,∠BAC=110°,试求∠PAO的度数.(不用写过程,直接写出答案)
(3)在(2)中,若无AB=AC的条件,你运能求出∠PAO的度数吗?若能,请求出来;若不能,请说明理由.
参考答案:
【答案】(1)10cm;(2)40°;(3)能,理由见解析.
【解析】
试题分析:(1)根据线段垂直平分线上的点到线段两端点的距离相等可得AP=BP,AO=CO,然后求出△PAO的周长=BC;
(2)根据等腰三角形两底角相等求出∠B、∠C的度数,再根据等边对等角的性质求出∠BAP,∠CAO,然后进行计算即可得解;
(3)先根据三角形的内角和等于180°求出∠B+∠C,再求出∠BAP+∠CAO,然后求解即可.
试题解析:(1)∵MP,NO分别垂直平分AB,AC,
∴AP=BP,AO=CO,
∴△PAO的周长=AP+PO+AO=BO+PO+OC=BC,
∵BC=1Ocm,
∴△PAO的周长10cm;
(2)∵AB=AC,∠BAC=110°,
∴∠B=∠C=![]() (180°-110°)=35°,
(180°-110°)=35°,
∵MP,NO分别垂直平分AB,AC,
∴AP=BP,AO=CO,
∴∠BAP=∠B=35°,∠CAO=∠C=35°,
∴∠PAO=∠BAC-∠BAP-∠CAO=110°-35°-35°=40°;
(3)能.理由如下:
∵∠BAC=110°,
∴∠B+∠C=180°-110°=70°,
∵MP,NO分别垂直平分AB,AC,
∴AP=BP,AO=CO,
∴∠BAP=∠B,∠CAO=∠C,
∴∠PAO=∠BAC-∠BAP-∠CAO=∠BAC-(∠B+∠C)=110°-70°=40°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知ABCD中,∠A+∠C=100°,则∠B的度数是( )
A. 60° B. 100°
C. 130° D. 160°
-
科目: 来源: 题型:
查看答案和解析>>【题目】某省进入全民医保改革3年来,共投入36400000元,将36400000用科学记数法表示为。
-
科目: 来源: 题型:
查看答案和解析>>【题目】正三角形、正方形、等腰直角三角形、平行四边形中,既是轴对称图形又是中心对称图形的是( )
A.正三角形
B.正方形
C.等腰直角三角形
D.平行四边形 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图, 在□ABCD中,点E、F是AD、BC的中点,连接BE、DF.
(1)求证:BE=DF.
(2)若BE平分∠ABC且交边AD于点E,AB=6cm,BC=10cm,试求线段DE的长.

-
科目: 来源: 题型:
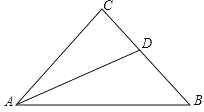
查看答案和解析>>【题目】如图,在△ABC中,AC=BC,AD平分∠BAC,∠ADC=60°,求∠C的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】你能求(x﹣1)(x99+x98+x97+…+x+1)的值吗?遇到这样的问题,我们可以先思考一下,从简单的情形入手.先分别计算下列各式的值:
①(x﹣1)(x+1)=x2﹣1;
②(x﹣1)(x2+x+1)=x3﹣1;
③(x﹣1)(x3+x2+x+1)=x4﹣1;
…
由此我们可以得到:(x﹣1)(x99+x98+x97+…+x+1)= .
请你利用上面的结论,再完成下面两题的计算:
(1)(﹣2)50+(﹣2)49+(﹣2)48+…+(﹣2)+1.
(2)若x3+x2+x+1=0,求x2016的值.
相关试题

