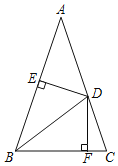
【题目】如图,△ABC中,AB=AC,∠A=36°,D是AC上一点,且BD=BC,过点D分别作DE⊥AB,DF⊥BC,垂足分別是E,F,下列结论:①BD是∠ABC的平分线;②D是AC的中点;③DE垂直平分AB;④AB=BC+CD;其中正确的结论是_____(填序号).
【答案】①③④
【解析】
根据等腰三角形的性质可得∠ABC=∠C=∠BDC=72°,利用外角性质可得∠ABD=36°,可得∠ABD=∠A=∠DBC=36°,根据等腰三角形的性质对各选项逐一判定即可得答案.
①∵∠A=36°,AB=AC,
∴∠ABC=∠C=72°,
∵BD=BC,
∴∠BDC=∠C=72°,
∵∠BDC=∠A+∠ABD,
∴∠ABD=36°,
∴∠ABD=∠CBD=36°,即BD是∠ABC的平分线,①正确.
②∵∠A+∠ABD=36°,
∴AD=BD,
∵BD≠CD,
∴AD≠CD,故②错误;
③∵∠ABD=∠A=36°,
∴AD=BD,
∵DE⊥AB,
∴AE=BE,
∴DE垂直平分AB,③正确;
④由①③可知,AD=BD=BC,
∵AB=AC,
∴AB=AD+CD=BC+CD,④正确;
综上所述,正确的结论有①③④,
故答案为:①③④.

