Question

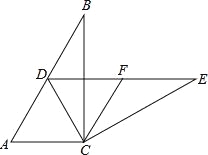
【题目】如图，在Rt△ABC中，∠ACB=90°，∠B=30°，将△ABC绕点C按顺时针方向旋转n度后，得到△DEC，点D刚好落在AB边上．

（1）求n的值；

（2）若F是DE的中点，判断四边形ACFD的形状，并说明理由．

Answer 1

【答案】(1)、n=60；(2)、菱形；证明过程见解析

【解析】

试题分析：(1)、利用旋转的性质得出AC=CD，进而得出△ADC是等边三角形，即可得出∠ACD的度数；

(2)、利用直角三角形的性质得出FC=DF，进而得出AD=AC=FC=DF，即可得出答案．

试题解析：(1)、∵在Rt△ABC中，∠ACB=90°，∠B=30°，将△ABC绕点C按顺时针方向旋转n度后，得到△DEC， ∴AC=DC，∠A=60°， ∴△ADC是等边三角形， ∴∠ACD=60°， ∴n的值是60；

(2)、四边形ACFD是菱形； 理由：∵∠DCE=∠ACB=90°，F是DE的中点， ∴FC=DF=FE，

∵∠CDF=∠A=60°， ∴△DFC是等边三角形， ∴DF=DC=FC， ∵△ADC是等边三角形，

∴AD=AC=DC， ∴AD=AC=FC=DF， ∴四边形ACFD是菱形．