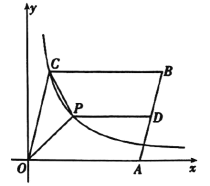
【题目】如图，的边在轴的正半轴上，，反比例函数()的图象经过点．

(1)求反比例函数的关系式和点的坐标，

(2)过的中点作轴交反比例函数图象于点，连接．求△的面积．

【答案】（1），B(6，4)；（2）3

【解析】

（1）由点A的坐标利用反比例函数图象上点的坐标特征即可求出反比例函数关系式，再根据平行四边形的性质结合点A、O、C的坐标即可求出点B的坐标；（2）延长DP交OC于点E，由点D为线段BA的中点，可求出点D的坐标，再令反比例函数关系式中y=2求出x值即可得出点P的坐标，由此即可得出PD、EP的长度，根据三角形的面积公式即可得出结论；

（1）∵反比例函数y=（x>0）的图象经过点C（1，4），

∴m=1×4=4，

∴反比例函数的关系式为y=（x>0）．

∵四边形OABC为平行四边形，且点O（0，0），OA=5，点C（1，4），

∴点B（6，4）．

（2）延长DP交OC于点E，如图所示．

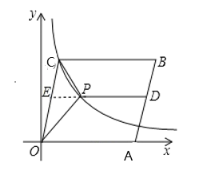
∵点D为线段AB的中点，点A（5，0）、B（6，4），

∴点D（ ，2）．

令y=中y=2，则x=2，

∴点P（2，2），

∴PD=-2=，EP=ED-PD=，

∴S△COP= EP（yC-yO）=××（4-0）=3．

关闭