【题目】Pn表示n边形的对角线的交点个数(指落在其内部的交点),如果这些交点都不重合,那么Pn与n的关系式是:Pn= ![]() (n2﹣an+b)(其中a,b是常数,n≥4)
(n2﹣an+b)(其中a,b是常数,n≥4)
(1)通过画图,可得:四边形时,P4= ;五边形时,P5=
(2)请根据四边形和五边形对角线交点的个数,结合关系式,求a,b的值.
参考答案:
【答案】
(1)1;5
(2)
解:将(1)中的数值代入公式,
得: 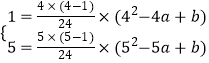 ,
,
解得: ![]()
【解析】解:(1)画出图形如下.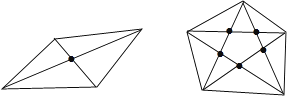
由画形,可得:
当n=4时,P4=1;当n=5时,P5=5.
故答案为:1;5.
(1)依题意画出图形,数出图形中对角线交点的个数即可得出结论;(2)将(1)中的数值代入公式可得出关于a、b的二元一次方程组,解方程组即可得出结论.本题考查了多边形的对角线、作图以及二元一次方程组的应用,解题的关键是:(1)画出图形,数出对角线交点的个数;(2)代入数据得出关于a、b的二元一次方程组.本题属于基础题,难度不大,解决该题型题目时,依据题意画出图形,利用数形结合解决问题是关键.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直角坐标系中,△ABC的顶点都在网格点上,其中,C点坐标为(1,2).

(1)写出点A、B的坐标:
(2)将△ABC先向左平移2个单位长度,再向上平移1个单位长度,得到△A′B′C′,则A′B′C′的三个顶点坐标分别是A′(,)、B′(,)、C′(,).
(3)△ABC的面积为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】由一些相同的小正方体搭成的几何体的左视图和俯视图如图所示,请在网格中涂出一种该几何体的主视图,且使该主视图是轴对称图形.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(﹣3,5),B(﹣2,1),C(﹣1,3).

(1)若△ABC经过平移后得到△A1B1C1 , 已知点C1的坐标为(4,0),写出顶点A1 , B1的坐标;
(2)若△ABC和△A1B2C2关于原点O成中心对称图形,写出△A1B2C2的各顶点的坐标;
(3)将△ABC绕着点O按顺时针方向旋转90°得到△A2B3C3 , 写出△A2B3C3的各顶点的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,已知△ABC三个顶点的坐标分别是A(2,2),B(4,0),C(4,﹣4)
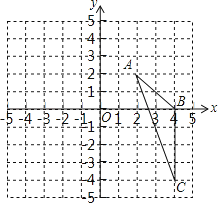
(1)请画出△ABC向左平移6个单位长度后得到的△A1B1C1;
(2)以点O为位似中心,将△ABC缩小为原来的 ,得到△A2B2C2 , 请在y轴右侧画出△A2B2C2 , 并求出∠A2C2B2的正弦值.
,得到△A2B2C2 , 请在y轴右侧画出△A2B2C2 , 并求出∠A2C2B2的正弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图△ABC三个顶点的坐标分别为A(0,﹣3)、B(3,﹣2)、C(2,﹣4),正方形网格中,每个小正方形的边长是1个单位长度.
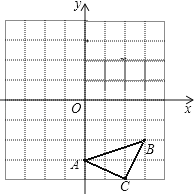
(1)画出△ABC向上平移6个单位得到的△A1B1C1;
(2)以点C为位似中心,在网格中画出△A2B2C2 , 使△A2B2C2与△ABC位似,且△A2B2C2与△ABC的位似比为2:1,并直接写出点A2的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,直角△ABC的三个顶点分别是A(﹣3,1),B(0,3),C(0,1)
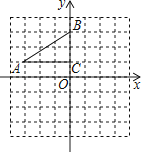
(1)将△ABC以点C为旋转中心旋转180°,画出旋转后对应的△A1B1C1;
(2)分别连结AB1、BA1后,求四边形AB1A1B的面积.
相关试题

