【题目】如图.矩形纸片ABCD中,已知AD=8,折叠纸片使AB边与对角线AC重合,点B落在点F处,折痕为AE,且EF=3.则AB的长为( )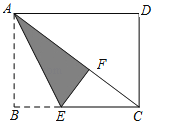
A.3
B.4
C.5
D.6
参考答案:
【答案】D
【解析】解:∵四边形ABCD是矩形,AD=8,
∴BC=8,
∵△AEF是△AEB翻折而成,
∴BE=EF=3,AB=AF,△CEF是直角三角形,
∴CE=8﹣3=5,
在Rt△CEF中,CF=![]() =4,
=4,
设AB=x,
在Rt△ABC中,AC2=AB2+BC2 , 即(x+4)2=x2+82 , 解得x=6,
故选:D.
先根据矩形的特点求出BC的长,再由翻折变换的性质得出△CEF是直角三角形,利用勾股定理即可求出CF的长,再在△ABC中利用勾股定理即可求出AB的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】“五四”青年节,市团委组织部分中学的团员去西山植树.某校九年级(3)班团支部领到一批树苗,若每人植4棵树,还剩37棵;若每人植6棵树,则最后一人有树植,但不足3棵,这批树苗共有__棵.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校规定学生的学期数学成绩满分为100分,其中平时学习成绩占30%,期末卷面成绩占70%,小明的两项成绩(百分制)依次是80分,90分,则小明这学期的数学成绩是( )
A. 83分B. 86分C. 87分D. 92.4分
-
科目: 来源: 题型:
查看答案和解析>>【题目】据调查,超速行驶是引发交通事故的主要原因之一.上周末,小明和三位同学用所学过的知识在一条笔直的道路上检测车速.如图,观测点C到公路的距离CD为100米,检测路段的起点A位于点C的南偏西60°方向上,终点B位于点C的南偏西45°方向上.某时段,一辆轿车由西向东匀速行驶,测得此车由A处行驶到B处的时间为4秒. 问此车是否超过了该路段16米/秒的限制速度?(参考数据:
 ≈1.4,
≈1.4,  ≈1.7)
≈1.7) 
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列判断正确的是( )
A. 一组对边平行,另一组对边相等的四边形一定是平行四边形
B. 两条对角线互相平分的四边形一定是平行四边形
C. 两组邻角分别互补的四边形一定是平行四边形
D. 两条对角线相等的四边形一定是平行四边形
-
科目: 来源: 题型:
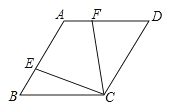
查看答案和解析>>【题目】如图,在菱形ABCD中,若∠B=60°,点E、F分别在AB、AD上,且BE=AF,则∠AEC+∠AFC的度数等于( )
A.120°
B.140°
C.160°
D.180° -
科目: 来源: 题型:
查看答案和解析>>【题目】若(x﹣5)(x+2)=x2+px+q,则p、q的值是( )
A.3,10
B.﹣3,﹣10
C.﹣3,10
D.3,﹣10
相关试题

