【题目】如图,△ABC中,∠ABC和∠ACB的角平分线BE、CF相交于点I,

(1)∠BIC=120°,求∠A的度数
(2)当∠BIC=135°,则∠A= 。
(3)请你用数学表达式归纳出∠BIC与∠A的关系式,并说明理由。
参考答案:
【答案】(1)60° (2)120° (3)∠BIC=90°+![]() ∠A.或∠A =2∠BIC - 180°
∠A.或∠A =2∠BIC - 180°
【解析】试题(1)根据题目给出的数据,可以知道∠A=![]() ;(2)总结上述的规律可得出∠A的值;(3)根据三角形的内角和定理用 ∠A表示出
;(2)总结上述的规律可得出∠A的值;(3)根据三角形的内角和定理用 ∠A表示出
∠ABC+∠ACB,再根据角平分线的定义表示出∠IEC+∠ICE,然后再利用三角形内角和定理即可得出结论.
试题解析:
(1)由题意得,∵∠BIC是△CEI的外角,
∴∠BIC=∠IEC+∠ICE(三角形外角定理),
∵∠IEC是△ABE的外角,
∴∠IDC=∠A+∠ABD(三角形外角定理),
∵BI、CI是∠ABC、∠ACB的平分线,
∴∠ABE=![]() ∠ABC,∠ICE=
∠ABC,∠ICE=![]() ∠ACB(角平分线定义),
∠ACB(角平分线定义),
∴∠BIC=![]() (∠ABC+∠ACB)+∠A=
(∠ABC+∠ACB)+∠A=![]() (
(![]() ∠A)+∠A=
∠A)+∠A=![]() +
+![]() ∠A
∠A
![]()
(2)由题意得,∵∠BIC是△CEI的外角,
∴∠BIC=∠IEC+∠ICE(三角形外角定理),
∵∠IEC是△ABE的外角,
∴∠IDC=∠A+∠ABD(三角形外角定理),
∵BI、CI是∠ABC、∠ACB的平分线,
∴∠ABE=![]() ∠ABC,∠ICE=
∠ABC,∠ICE=![]() ∠ACB(角平分线定义),
∠ACB(角平分线定义),
∴∠BIC=![]() (∠ABC+∠ACB)+∠A=
(∠ABC+∠ACB)+∠A=![]() (
(![]() ∠A)+∠A=
∠A)+∠A=![]() +
+![]() ∠A
∠A
![]()
(3) 根据上述规律可得,∠BIC=90°+![]() ∠A.或∠A =2∠BIC - 180°
∠A.或∠A =2∠BIC - 180°
理由如下:
∵∠BIC是△CEI的外角,
∴∠BIC=∠IEC+∠ICE(三角形外角定理),
∵∠IEC是△ABE的外角,
∴∠IDC=∠A+∠ABD(三角形外角定理),
∵BI、CI是∠ABC、∠ACB的平分线,
∴∠ABE=![]() ∠ABC,∠ICE=
∠ABC,∠ICE=![]() ∠ACB(角平分线定义),
∠ACB(角平分线定义),
∴∠BIC=![]() (∠ABC+∠ACB)+∠A=
(∠ABC+∠ACB)+∠A=![]() (
(![]() ∠A)+∠A=
∠A)+∠A=![]() +
+![]() ∠A.
∠A.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(
 )﹣1﹣(3﹣
)﹣1﹣(3﹣  )0﹣2sin60°+|
)0﹣2sin60°+|  ﹣2|
﹣2| -
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,AB=AC,点D是直线BC上一点(不与B、C重合),以AD为一边在AD的右侧作△ADE,使AD=AE,∠DAE=∠BAC,连接CE.
(1)如图一,若△ABC是等边三角形,且AB=AC=2,点D在线段BC上,
①求证:∠BCE+∠BAC=180°;
②当四边形ADCE的周长取最小值时,求BD的长.
(2)若∠BAC
 60° ,当点D在射线BC上移动,则∠BCE和∠BAC 之间有怎样的数量关系?并说明理由.
60° ,当点D在射线BC上移动,则∠BCE和∠BAC 之间有怎样的数量关系?并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的方程x2﹣3mx+2(m﹣1)=0的两根为x1、x2 , 且
 +
+  =﹣
=﹣  ,则m的值是多少?
,则m的值是多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在△ABC中,AB=AC,BD⊥AC于D,CE⊥AB于E,BD,CE相交于F.
求证:AF平分∠BAC.

-
科目: 来源: 题型:
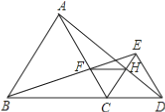
查看答案和解析>>【题目】如图,已知点B、C、D在同一条直线上,△ABC和△CDE都是等边三角形.BE交AC于F,AD交CE于H,求证:
(1)△BCE≌△ACD;
(2)CF=CH;
(3)△FCH是等边三角形;
(4)FH∥BD.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,CD⊥AB,EF⊥AB,垂足分别为D、F,∠1=∠2,
(1)试判断DG与BC的位置关系,并说明理由.
(2)若∠A=70°,∠BCG=40°,求∠AGD的度数.

相关试题

