

| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 2 |
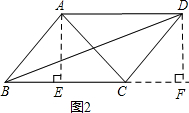
| 2b2+2c2-a2 |


科目:初中数学 来源: 题型:
| 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源:2011年安徽省马鞍山市成功学校中考数学一模试卷(解析版) 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:
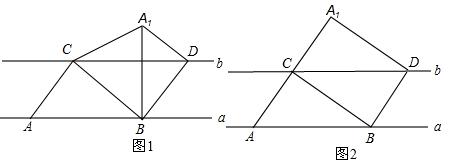
如图,A、B是直线![]() 上的两个定点,点C、D在直线
上的两个定点,点C、D在直线![]() 上运动(点C在点D的左侧),AB=CD=6cm,已知
上运动(点C在点D的左侧),AB=CD=6cm,已知![]() //
//![]() ,连接AC、BD、BC,把
,连接AC、BD、BC,把![]() 沿BC折叠得
沿BC折叠得![]() .
.
问题1:当![]() 、D两点重合时,则AC=___________cm;
、D两点重合时,则AC=___________cm;
问题2:当![]() 、D两点不重合时,连接
、D两点不重合时,连接![]() ,可探究发现
,可探究发现![]() ,
,
下面是小明的思考:
(1)将![]() 沿BC翻折,点A关于直线BC的对称点为
沿BC翻折,点A关于直线BC的对称点为![]() ,连接
,连接![]() 交BC所在直线于点M,由轴对称的性质,得
交BC所在直线于点M,由轴对称的性质,得![]() ,这一关系在变化过程中保持不变.
,这一关系在变化过程中保持不变.
(2)因为四边形ABCD是平行四边,设对角线的交点是O,易知![]() ,这一关系在变化过程中也保持不变。
,这一关系在变化过程中也保持不变。
请你借助于小明的思考,说明![]() 的理由。
的理由。
问题3:当![]() 、D两点不重合时,若直线
、D两点不重合时,若直线![]() 间的距离为
间的距离为![]() cm,且以点
cm,且以点![]() 为顶点的四边形是矩形,求AC的长。
为顶点的四边形是矩形,求AC的长。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com