搜索
如图，已知动点P在函数y=| 1 |
| 2x |
| A、4 | ||
| B、2 | ||
| C、1 | ||
D、
|
分析：由于P的坐标为（a，
），且PN⊥OB，PM⊥OA，那么N的坐标和M点的坐标都可以a表示，那么BN、NF、BN的长度也可以用a表示，接着F点、E点的也可以a表示，然后利用勾股定理可以分别用a表示AF，BE，最后即可求出AF•BE．
| 1 |
| 2a |
解答：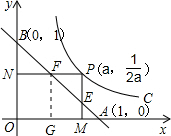
解：作FG⊥x轴，
∵P的坐标为（a，
），且PN⊥OB，PM⊥OA，
∴N的坐标为（0，
），M点的坐标为（a，0），
∴BN=1-
，
在直角三角形BNF中，∠NBF=45°（OB=OA=1，三角形OAB是等腰直角三角形），
∴NF=BN=1-
，
∴F点的坐标为（1-
，
），
同理可得出E点的坐标为（a，1-a），
∴AF2=（1-1+
）2+（
）2=
，BE2=（a）2+（-a）2=2a2，
∴AF2•BE2=
•2a2=1，即AF•BE=1．
故选C．
解：作FG⊥x轴，∵P的坐标为（a，
| 1 |
| 2a |
∴N的坐标为（0，
| 1 |
| 2a |
∴BN=1-
| 1 |
| 2a |
在直角三角形BNF中，∠NBF=45°（OB=OA=1，三角形OAB是等腰直角三角形），
∴NF=BN=1-
| 1 |
| 2a |
∴F点的坐标为（1-
| 1 |
| 2a |
| 1 |
| 2a |
同理可得出E点的坐标为（a，1-a），
∴AF2=（1-1+
| 1 |
| 2a |
| 1 |
| 2a |
| 1 |
| 2a2 |
∴AF2•BE2=
| 1 |
| 2a2 |
故选C．
点评：本题的关键是通过反比例函数上的点P来确定E、F两点的坐标，进而通过坐标系中两点的距离公式得出所求的值．
