【题目】如图,A为⊙O外一点,AB切⊙O于点B,AO交⊙O于C,CD⊥OB于E,交⊙O于点D,连接OD.若AB=12,AC=8.
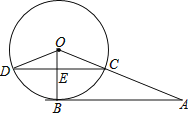
(1)求OD的长;
(2)求CD的长.
参考答案:
【答案】(1)5;(2)![]() .
.
【解析】
试题分析:(1)设⊙O的半径为R,根据切线定理得OB⊥AB,则在Rt△ABO中,利用勾股定理得到R2+122=(R+8)2,解得R=5,即OD的长为5;
(2)根据垂径定理由CD⊥OB得DE=CE,再证明△OEC∽△OBA,利用相似比可计算出CE=![]() ,所以CD=2CE=
,所以CD=2CE=![]() .
.
解:(1)设⊙O的半径为R,
∵AB切⊙O于点B,
∴OB⊥AB,
在Rt△ABO中,OB=R,AO=OC+AC=R+8,AB=12,
∵OB2+AB2=OA2,
∴R2+122=(R+8)2,
解得R=5,
∴OD的长为5;
(2)∵CD⊥OB,
∴DE=CE,
而OB⊥AB,
∴CE∥AB,
∴△OEC∽△OBA,
∴![]() =
=![]() ,
,
即![]() =
=![]() ,
,
∴CE=![]() ,
,
∴CD=2CE=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,y关于x的二次函数y=﹣
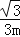 (x+m)(x﹣3m)图象的顶点为M,图象交x轴于A、B两点,交y轴正半轴于D点.以AB为直径作圆,圆心为C.定点E的坐标为(﹣3,0),连接ED.(m>0)
(x+m)(x﹣3m)图象的顶点为M,图象交x轴于A、B两点,交y轴正半轴于D点.以AB为直径作圆,圆心为C.定点E的坐标为(﹣3,0),连接ED.(m>0)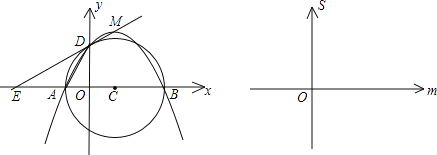
(1)写出A、B、D三点的坐标;
(2)当m为何值时M点在直线ED上?判定此时直线与圆的位置关系;
(3)当m变化时,用m表示△AED的面积S,并在给出的直角坐标系中画出S关于m的函数图象的示意图.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在边长为1的小正方形组成的方格纸中,有一个以格点为顶点的△ABC.
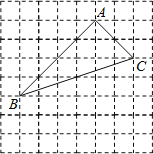
(1)试根据三角形三边关系,判断△ABC的形状;
(2)在方格纸中利用直尺分别画出AB、BC的垂直平分线,交点为O.观察点O的位置,你能得出怎样的结论?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线AB、CD相交于点O,∠BOE=90°,OM平分∠AOD,ON平分∠DOE.
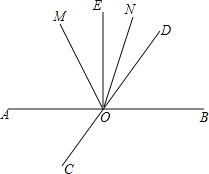
(1)若∠EON=18°,求∠AOC的度数.
(2)试判断∠MON与∠AOE的数量关系,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法不正确的是( )
A. 0既不是正数,也不是负数
B. 绝对值最小的数是0
C. 绝对值等于自身的数只有0和1
D. 平方等于自身的数只有0和1
-
科目: 来源: 题型:
查看答案和解析>>【题目】在红城中学举行的“我爱祖国”征文活动中,七年级和八年级共收到征文118篇,且七年级收到的征文篇数是八年级收到的征文篇数的一半还少2篇,求七年级收到的征文有多少篇?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,线段AB=12cm,延长AB到点C,使BC=
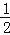 AB,点D是BC中点,点E是AD中点.
AB,点D是BC中点,点E是AD中点.
(1)根据题意,补全图形;
(2)求DE的长;
(3)若动点P从点A出发,以1cm/s的速度向点C运动,到达点C停止运动,点Q从点C出发,以2cm/s的速度向点A运动,到达点A停止运动,若运动时间为ts,当t为何值时,PQ=3cm?
相关试题

