【题目】如图,△ABC中,AB=AC,AD⊥BC,CE⊥AB,AE=CE.求证: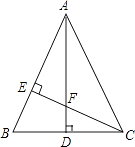
(1)△AEF≌△CEB;
(2)AF=2CD.
参考答案:
【答案】
(1)证明:∵AD⊥BC,CE⊥AB,
∴∠BCE+∠CFD=90°,∠BCE+∠B=90°,
∴∠CFD=∠B,
∵∠CFD=∠AFE,
∴∠AFE=∠B
在△AEF与△CEB中,
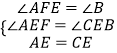 ,
,
∴△AEF≌△CEB(AAS)
(2)证明:∵AB=AC,AD⊥BC,
∴BC=2CD,
∵△AEF≌△CEB,
∴AF=BC,
∴AF=2CD
【解析】(1)根据垂直的定义得出∠BCE+∠CFD=90°,∠BCE+∠B=90°,根据同角的余角相等得出∠CFD=∠B,然后由AAS判断出△AEF≌△CEB;
(2)等腰三角形的三线合一得出BC=2CD,根据全等三角形的性质得出AF=BC,从而得出AF=2CD。
【考点精析】关于本题考查的余角和补角的特征和垂线的性质,需要了解互余、互补是指两个角的数量关系,与两个角的位置无关;垂线的性质:1、过一点有且只有一条直线与己知直线垂直.2、垂线段最短才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算a6×(a2)3÷a4的结果是( )
A. a3 B. a7 C. a8 D. a9
-
科目: 来源: 题型:
查看答案和解析>>【题目】杨华与季红用5张同样规格的硬纸片做拼图游戏,正面如图1所示,背面完全一样,将它们背面朝上搅匀后,同时抽出两张.规则如下:当两张硬纸片上的图形可拼成电灯或小人时,杨华得1分;当两张硬纸片上的图形可拼成房子或小山时,季红得1分(如图2).问题:游戏规则对双方公平吗?请说明理由;若你认为不公平,如何修改游戏规则才能使游戏对双方公平?

-
科目: 来源: 题型:
查看答案和解析>>【题目】春节前夕,某商店根据市场调查,用2000元购进第一批盒装花,上市后很快售完,接着又用4200元购进第二批这种盒装花.已知第二批所购的盒数是第一批所购花盒数的3倍,且每盒花的进价比第一批的进价少6元.求第一批盒装花每盒的进价.
-
科目: 来源: 题型:
查看答案和解析>>【题目】《云南省“十三五”规划纲要》中指出:到2020年,昆明中心城市人口达到400万人左右.将400万用科学记数法表示为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】净水机的核心部件就是水处理反渗透膜,水处理反渗透膜就像是一个筛子,它的孔径只有0.11纳米,水在压力的作用下一层层过滤,离子以上的杂质像抗生素、重金属、细菌等都能过滤掉,0.11纳米即0.00000000011米,将0.11纳米用科学记数法表示为( )
A.1.1×10﹣9米
B.1.1×10﹣10米
C.11×10﹣9米
D.0.11×10﹣9米 -
科目: 来源: 题型:
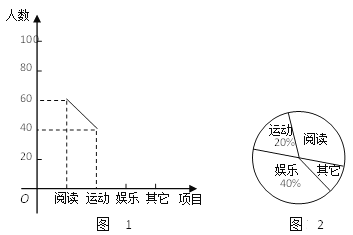
查看答案和解析>>【题目】某中学团委会为研究该校学生的课余活动情况,采取抽样的方法,从阅读、运动、娱乐、其它等四个方面调查了若干名学生的兴趣爱好,并将调查的结果绘制了如下的两幅不完整的统计图(如图1,图2),请你根据图中提供的信息解答下列问题:
(1)在这次研究中,一共调查了多少名学生?
(2)“其它”在扇形图中所占的圆心角是多少度?
(3)补全频数分布折线图.
相关试题

