【题目】已知:抛物线y=x2+(b﹣1)x﹣5.
(1)写出抛物线的开口方向和它与y轴交点的坐标;
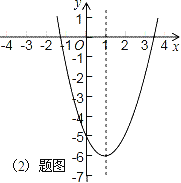
(2)若抛物线的对称轴为直线x=1,求b的值,并画出抛物线的草图(不必列表);
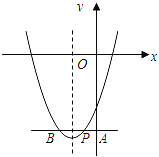
(3)如图,若b>3,过抛物线上一点P(﹣1,c)作直线PA⊥y轴,垂足为A,交抛物线于另一点B,且BP=2PA,求这条抛物线所对应的二次函数解析式.
参考答案:
【答案】(1)、开口向上;(0,﹣5);(2)、b=1;图形见解析;(3)、y=x2+4x﹣5
【解析】
试题分析:(1)、根据a值大于0,判断抛物线的开口向上,令x=0求出函数值y,就是抛物线与y轴的交点坐标;(2)、根据对称轴解析式列式求出b的值,从而得到抛物线解析式,再根据抛物线与坐标轴的交点与顶点坐标作出草图即可;(3)、先根据b>3判断出点P在对称轴的左侧,然后根据BP=2PA求出点B的坐标,然后把点P、B的坐标代入抛物线解析式,利用待定系数法求出b、c的值,即可写出该抛物线对应的二次函数解析式.[或者根据点BP的中点在抛物线的对称轴上,利用对称轴解析式列式进行计算求解b的值.
试题解析:(1)、∵a=1>0, ∴抛物线开口向上, 当x=0时,y=02+(b﹣1)×0﹣5=﹣5,
∴它与y轴的交点坐标为(0,﹣5);
(2)、抛物线的对称轴为x=1, ∴﹣![]() =﹣
=﹣![]() =1, 解得b=﹣1,故抛物线的解析式为y=x2﹣2x﹣5;
=1, 解得b=﹣1,故抛物线的解析式为y=x2﹣2x﹣5;
图象如右;
(3)、∵b>3, ∴抛物线的对称轴x=﹣![]() =﹣
=﹣![]() <﹣1, ∴对称轴在点P的左侧,
<﹣1, ∴对称轴在点P的左侧,
∵直线PA⊥y轴,且P(﹣1,c),BP=2PA, ∴点B的坐标为(﹣3,c),
把点B(﹣3,c)、P(﹣1,c)代入抛物线解析式y=x2+(b﹣1)x﹣5得b=5,c=-8
∴抛物线所对应的二次函数解析式为y=x2+4x﹣5;
-
科目: 来源: 题型:
查看答案和解析>>【题目】若等腰三角形的顶角为80°,则它的底角度数为( )
A. 80° B. 50° C. 40° D. 20°
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知|ab﹣2|+(b﹣1)2=0
(1)求a,b的值;
(2)求b2004+(﹣b)2005的值;
(3)求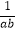 +
+ 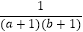 +
+ 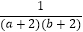 +…+
+…+ 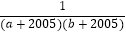 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】计算
(1)2+(﹣6)﹣(﹣3)
(2)2×9÷(﹣ )×3
)×3
(3)(﹣5)×7+(﹣125)÷(﹣6 )
)
(4)﹣22+24÷4×(﹣3)2 . -
科目: 来源: 题型:
查看答案和解析>>【题目】平面直角坐标系中,已知ABCD的三个顶点坐标分别是A(m,n),B(2,﹣1),C(﹣m,﹣n),则点D的坐标是( )
A.(﹣2,1)
B.(﹣2,﹣1)
C.(﹣1,﹣2)
D.(﹣1,2) -
科目: 来源: 题型:
查看答案和解析>>【题目】若|a|>a,则a是( )
A.正数
B.负数
C.非正数
D.非负数 -
科目: 来源: 题型:
查看答案和解析>>【题目】最小的正整数是
A. 0 B. 1 C. 2 D. -1
相关试题

