【题目】已知方程x2+2kx+k2﹣2k+1=0有两个实数根x1 , x2 .
(1)求实数k的取值范围;
(2)若x12+x22=4,求k的值.
参考答案:
【答案】
(1)解:根据题意得△=(2k)2﹣4(k2﹣2k+1)=8k﹣4≥0,
解得k≥ ![]() ;
;
(2)解:根据题意得x1+x2=﹣2k,x1x2=k2﹣2k+1,
∵x12+x22=4,
∴(x1+x2)2﹣2x1x2=4
∴4k2﹣2(k2﹣2k+1)=4,
整理得k2+2k﹣3=0,解得k1=﹣3,k2=1,
而k≥ ![]()
∴k=1.
【解析】(1)根据判别式的意义得到△=(2k)2﹣4(k2﹣2k+1)=8k﹣4≥0,然后解不等式即可;(2)根据根与系数的关系得到x1+x2=﹣2k,x1x2=k2﹣2k+1,再利用完全平方公式由x12+x22=4得到(x1+x2)2﹣2x1x2=4,则4k2﹣2(k2﹣2k+1)=4,然后解关于k的方程,最后利用k的范围可确定满足条件的k的值.
【考点精析】关于本题考查的求根公式和根与系数的关系,需要了解根的判别式△=b2-4ac,这里可以分为3种情况:1、当△>0时,一元二次方程有2个不相等的实数根2、当△=0时,一元二次方程有2个相同的实数根3、当△<0时,一元二次方程没有实数根;一元二次方程ax2+bx+c=0(a≠0)的根由方程的系数a、b、c而定;两根之和等于方程的一次项系数除以二次项系数所得的商的相反数;两根之积等于常数项除以二次项系数所得的商才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,动点M、N同时从原点出发沿数轴做匀速运动,己知动点M、N的运动速度比是1:2(速度单位:1个单位长度/秒),设运动时间为t秒.
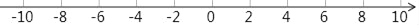
(1)若动点M向数轴负方向运动,动点N向数轴正方向运动,当t=2秒时,动点M运动到A点,动点N运动到B点,且AB=12(单位长度).
①在直线l上画出A、B两点的位置,并回答:点A运动的速度是 (单位长度/秒);点B运动的速度是 (单位长度/秒).
②若点P为数轴上一点,且PA﹣PB=OP,求
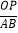 的值;
的值;(2)由(1)中A、B两点的位置开始,若M、N同时再次开始按原速运动,且在数轴上的运动方向不限,再经过几秒,MN=4(单位长度)?
-
科目: 来源: 题型:
查看答案和解析>>【题目】汽车的“燃油效率”是指汽车每消耗1升汽油行驶的里程数. “燃油效率”越高表示汽车每消耗1升汽油行驶的里程数越多;“燃油效率”越低表示汽车每消耗1升汽油行驶的里程数越少. 下图描述了甲、乙、丙三辆汽车在不同速度下的燃油效率情况.
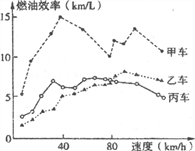
根据图中提供的信息,下列说法:
①以相同速度行驶相同路程,三辆车中,甲车消耗汽油最多
②以低于80km/h的速度行驶时,行驶相同路程,三辆车中,乙车消耗汽油最少
③以高于80km/h的速度行驶时,行驶相同路程,乙车比丙车省油
④以80km/h的速度行驶时,行驶100公里,甲车消耗的汽油量约为10升
正确的是________(填写正确结论的序号).
-
科目: 来源: 题型:
查看答案和解析>>【题目】2017年5月,“一带一路”国际合作高峰论坛在中国北京成功召开. 会议期间为方便市民出行,某路公交车每天比原来的运行增加30车次. 经调研得知,原来这路公交车平均每天共运送乘客5600人,高峰论坛期间这路公交车平均每天共运送乘客8000人,且平均每车次运送乘客与原来的数量基本相同,问高峰论坛期间这路公交车每天运行多少车次?
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)已知am=2,an=3.求am+n的值;
(2)已知n为正整数,且x2n=7.求7(x3n)2﹣3(x2)2n的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】画出函数
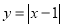 的图象.
的图象. (1)函数
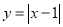 的自变量x的取值范围是________;
的自变量x的取值范围是________;(2)列表(把表格补充完整)
x
……
-2
-1
0
1
2
3
4
……
y
(3)描点、连线
(4)结合图象,写出函数的一条性质________________________________________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线AE与CD相交于点B,射线BF平分∠ABC,射线BG在∠ABD内,
(1)若∠DBE的补角是它的余角的3倍,求∠DBE的度数;
(2)在(1)的件下,若∠DBG=∠ABG﹣33°,求∠ABG的度数;
(3)若∠FBG=100°,求∠ABG和∠DBG的度数的差.

相关试题

