搜索
【题目】在如图的4×3网格中，每个小正方形的边长均为1，正方形顶点叫网格格点，连结两个网格格点的线段叫网格线段．
（1）请你画一个边长为
的菱形，并求其面积；
（2）若a是图中能用网格线段表示的最大无理数，b是图中能用网格线段表示的最小无理数，求a2-2b2的平方根．
参考答案：
【答案】(1)作图见解析；4；（2）±4．
【解析】试题分析：
（1）直接利用勾股定理以及菱形的性质得出符合题意的图形求出其面积；
（2）利用网格直接得出最大的无理数以及最小的无理数，再利用平方根的定义得出即可．
试题解析：
（1）如图所示：
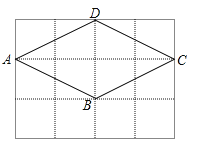
四边形ABCD是边长为
的菱形，
其面积为：
BD×AC=×2×4=4；
（2）由网格得出：
用网格线段表示的最大无理数为：
，
图中能用网格线段表示的最小无理数为：
，
∴a2-2b2=（
）2－2
＝16，
∴a2-2b2的平方根是：±4．
-
科目： 来源： 题型：
查看答案和解析>>【题目】三角形的三边长a，b，c满足2ab=（a+b）2﹣c2，则此三角形是（ ）
A. 钝角三角形 B. 锐角三角形 C. 直角三角形 D. 等边三角形
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图所示的一块地，∠ADC＝90°，AD＝12m，CD＝9m，AB＝39m，BC＝36m，求这块地的面积．
-
科目： 来源： 题型：
查看答案和解析>>【题目】一名射击爱好者5次射击的中靶环数如下：6，7，9，8，9．这5个数据的众数是________．
-
科目： 来源： 题型：
查看答案和解析>>【题目】阅读材料：小明在学习二次根式后，发现一些含根号的式子可以写成另一个式子的平方，如：3＋2
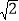＝(1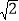＋)2，善于思考的小明进行了以下探索：设a＋b
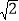＝(m＋n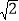)2(其中a、b、m、n均为整数)，则有a＋b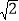＝m2＋2n2＋2mn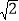.∴a＝m2＋2n2，b＝2mn.这样小明就找到了一种把部分a＋b
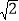的式子化为平方式的方法．请你仿照小明的方法探索并解决下列问题：
(1)当a、b、m、n均为正整数时，若a＋b
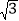＝(m＋n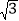)2，用含m、n的式子分别表示a、b，得a＝________，b＝________；(2)试着把7+4
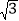化成一个完全平方式.（3）请化简：
． -
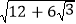科目： 来源： 题型：
查看答案和解析>>【题目】下列命题其中真命题的个数是（）
（1）长度相等的弧是等弧；
（2）圆是轴对称图形，它的对称轴是过圆心的弦
（3）相等的圆心角所所对的弦相等；
（4）在同圆或者等圆中，相等的两弦所对的弧相等．
A. 0 B. 1 C. 2 D. 3
-
科目： 来源： 题型：
查看答案和解析>>【题目】作图题的书写步骤是________、________、________，而且要画出________和________，保留________．
相关试题
