【题目】如图,抛物线y=ax2+2ax+1与x轴仅有一个公共点A,经过点A的直线交该抛物线于点B,交y轴于点C,且点C是线段AB的中点.
(1)求这条抛物线对应的函数解析式;
(2)求直线AB对应的函数解析式.
参考答案:
【答案】
(1)
解:∵抛物线y=ax2+2ax+1与x轴仅有一个公共点A,
∴△=4a2﹣4a=0,解得a1=0(舍去),a2=1,
∴抛物线解析式为y=x2+2x+1;
(2)
解:∵y=(x+1)2,
∴顶点A的坐标为(﹣1,0),
∵点C是线段AB的中点,
即点A与点B关于C点对称,
∴B点的横坐标为1,
当x=1时,y=x2+2x+1=1+2+1=4,则B(1,4),
设直线AB的解析式为y=kx+b,
把A(﹣1,0),B(1,4)代入得 ![]() ,解得
,解得 ![]() ,
,
∴直线AB的解析式为y=2x+2
【解析】(1)利用△=b2﹣4ac=0时,抛物线与x轴有1个交点得到4a2﹣4a=0,然后解关于a的方程求出a,即可得到抛物线解析式;(2)利用点C是线段AB的中点可判断点A与点B的横坐标互为相反数,则可以利用抛物线解析式确定B点坐标,然后利用待定系数法求直线AB的解析式.本题考查了抛物线与x轴的交点:对于二次函数y=ax2+bx+c(a,b,c是常数,a≠0),△=b2﹣4ac决定抛物线与x轴的交点个数:△=b2﹣4ac>0时,抛物线与x轴有2个交点;△=b2﹣4ac=0时,抛物线与x轴有1个交点;△=b2﹣4ac<0时,抛物线与x轴没有交点.也考查了利用待定系数法求函数解析式.
【考点精析】利用确定一次函数的表达式和抛物线与坐标轴的交点对题目进行判断即可得到答案,需要熟知确定一个一次函数,需要确定一次函数定义式y=kx+b(k不等于0)中的常数k和b.解这类问题的一般方法是待定系数法;一元二次方程的解是其对应的二次函数的图像与x轴的交点坐标.因此一元二次方程中的b2-4ac,在二次函数中表示图像与x轴是否有交点.当b2-4ac>0时,图像与x轴有两个交点;当b2-4ac=0时,图像与x轴有一个交点;当b2-4ac<0时,图像与x轴没有交点.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下面是淄博市2016年4月份的天气情况统计表:
日期
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
天气
多云
阴
多云
晴
多云
阴
晴
晴
晴
多云
多云
多云
晴
晴
雨
日期
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
天气
雨
多云
多云
多云
多云
晴
多云
多云
晴
多云
多云
多云
晴
晴
晴
(1)请完成下面的汇总表:天气
晴
多云
阴
雨
天数
(2)根据汇总表绘制条形图;
(3)在该月中任取一天,计算该天多云的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在边长为1个单位长度的小正方形组成的网格中,点A、B、C都是格点.
(1)将△ABC向左平移6个单位长度得到△A 1B 1C 1,请在网格中画出△A 1B 1C 1
(2)将△ABC绕点O按逆时针方向旋转180°得到△A 2B 2C 2,请在网格画出△A 2B 2C 2.
(3)请问△A 1B 1C 1与△A 2B 2C 2成中心对称吗?

-
科目: 来源: 题型:
查看答案和解析>>【题目】某校随机抽取部分学生,就“学习习惯”进行调查,将“对自己做错的题目进行整理、分析、改正”
 选项为:很少、有时、常常、总是
选项为:很少、有时、常常、总是 的调查数据进行了整理,绘制成部分统计图如下:
的调查数据进行了整理,绘制成部分统计图如下: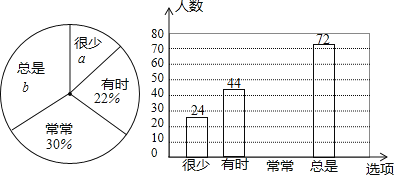
请根据图中信息,解答下列问题
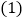 该调查的样本容量为______,
该调查的样本容量为______,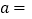 ______
______ ,
,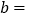 ______
______ ,“常常”对应扇形的圆心角为______
,“常常”对应扇形的圆心角为______
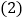 请你补全条形统计图;
请你补全条形统计图;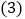 若该校共有3200名学生,请你估计其中“总是”对错题进行整理、分析、改正的学生有多少名?
若该校共有3200名学生,请你估计其中“总是”对错题进行整理、分析、改正的学生有多少名? -
科目: 来源: 题型:
查看答案和解析>>【题目】一辆客车从甲地开往乙地,车上原有(5a﹣2b)人,中途停车一次,有一些人下车,此时下车的人数比车上原有人数一半还多2人,同时又有一些上车,上车的人数比
 (7a﹣4b)少3人.
(7a﹣4b)少3人. (1)用代数式表示中途下车的人数;
(2)用代数式表示中途下车、上车之后,车上现在共有多少人?
(3)当a=10,b=9时,求中途下车、上车之后,车上现在的人数?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC,AD平分∠BAC交BC于点D,BC的中点为M,ME∥AD,交BA的延长线于点E,交AC于点F.

(1)求证:AE=AF;
(2)求证:BE= (AB+AC).
(AB+AC). -
科目: 来源: 题型:
查看答案和解析>>【题目】已知,点M是二次函数y=ax2(a>0)图象上的一点,点F的坐标为(0,
 ),直角坐标系中的坐标原点O与点M,F在同一个圆上,圆心Q的纵坐标为
),直角坐标系中的坐标原点O与点M,F在同一个圆上,圆心Q的纵坐标为  .
.
(1)求a的值;
(2)当O,Q,M三点在同一条直线上时,求点M和点Q的坐标;
(3)当点M在第一象限时,过点M作MN⊥x轴,垂足为点N,求证:MF=MN+OF.
相关试题

