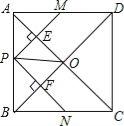
【题目】如图,在正方形ABCD中,点P是AB上一动点(不与A,B重合),对角线AC,BD相交于点O,过点P分别作AC,BD的垂线,分别交AC,BD于点E,F,交AD,BC于点M,N.下列结论:①△APE≌△AME;②PM+PN=AC;③PE2+PF2=PO2;④△POF∽△BNF;⑤当△PMN∽△AMP时,点P是AB的中点.其中正确的结论的个数有( )个.
A.5 B.4 C.3 D.2
参考答案:
【答案】B.
【解析】
试题分析:∵四边形ABCD是正方形,
∴∠BAC=∠DAC=45°.
∵在△APE和△AME中,
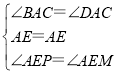 ,
,
∴△APE≌△AME,故①正确;
∴PE=EM=![]() PM,
PM,
同理,FP=FN=![]() NP.
NP.
∵正方形ABCD中AC⊥BD,
又∵PE⊥AC,PF⊥BD,
∴∠PEO=∠EOF=∠PFO=90°,且△APE中AE=PE
∴四边形PEOF是矩形.
∴PF=OE,
∴PE+PF=OA,
又∵PE=EM=![]() PM,FP=FN=
PM,FP=FN=![]() NP,OA=
NP,OA=![]() AC,
AC,
∴PM+PN=AC,故②正确;
∵四边形PEOF是矩形,
∴PE=OF,
在直角△OPF中,OF2+PF2=PO2,
∴PE2+PF2=PO2,故③正确.
∵△BNF是等腰直角三角形,而△POF不一定是,故④错误;
∵△AMP是等腰直角三角形,当△PMN∽△AMP时,△PMN是等腰直角三角形.
∴PM=PN,
又∵△AMP和△BPN都是等腰直角三角形,
∴AP=BP,即P时AB的中点.故⑤正确.
故选B.
考点: 1.相似三角形的判定与性质;2.全等三角形的判定与性质;3.勾股定理;4.正方形的性质.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,在正方形ABCD中,P是对角线AC上的一点,点E在BC的延长线上,且PE=PB.

(1)求证:△BCP≌△DCP;
(2)求证:∠DPE=∠ABC;
(3)把正方形ABCD改为菱形,其它条件不变(如图②),若∠ABC=58°,则∠DPE= 度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】2017年5月11时05分,昆明南至北京西G405/6次“世界的香格里拉”高铁旅游文化列车驶离昆明南站,驶向北京,这是云南首趟开往北京的高铁动车,北京西到昆明南G405高铁时刻表站点票价一览一等座:1877.5元,其中数据1877.5元保留2个有效数字用科学记数法表示为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】(-3)-=1 ;-7=-2 ;-5-=0
-
科目: 来源: 题型:
查看答案和解析>>【题目】世界上最高的山峰是珠穆朗玛峰,其海拔高度大约是8848m,吐鲁番盆地的海拔高度大约是-155m,两处高度相差m.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:-4+7-4= .
-
科目: 来源: 题型:
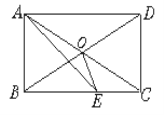
查看答案和解析>>【题目】如图,在矩形ABCD中,AC、BD相交于O,AE平分∠BAD,交BC于E,若∠CAE=15°,求∠BOE的度数.
相关试题

