【题目】某现代农业示范园区准备租用甲、乙两种货车将一批蔬菜运到城区销售,已知一辆甲种货车可装茄子4吨和玉米1吨,一辆乙种货车可装茄子和玉米各2吨,若园区要求安排甲,乙两种货车共10辆一次性运输茄子和玉米,其中茄子不少于30吨,玉米不少于13吨.
(1)那么园区如何安排甲,乙两种货车进行运输?有几种方案?
(2)若甲种货车每辆要付运输费300元,乙种货车每辆要付运输费280元,则园区应选择哪种方案,使运输费最少?最少运费是多少?
参考答案:
【答案】
(1)解:设安排甲种货车x辆,则安排乙种货车(10﹣x)辆,依题意得
![]() ,
,
解此不等式组得5≤x≤7.
∵x是正整数
∴x可取的值为5,6,7.
∴安排甲、乙两种货车有三种方案:
甲种货车 | 乙种货车 | |
方案一 | 5辆 | 5辆 |
方案二 | 6辆 | 4辆 |
方案三 | 7辆 | 3辆 |
(2)解:∵甲种货车每辆要付运输费300元,乙种货车每辆要付运输费280元,
∴选择方案一运费最少,最少运费是300×5+280×5=2900(元).
答:园区应选择方案一,使运输费最少,最少运费是2900元
【解析】(1)由题意列出不等式组,在解集内有几个整数解就有几种方案;(2)由已知算出每种方案的费用,比较得出最少运费方案.
【考点精析】根据题目的已知条件,利用一元一次不等式组的应用的相关知识可以得到问题的答案,需要掌握1、审:分析题意,找出不等关系;2、设:设未知数;3、列:列出不等式组;4、解:解不等式组;5、检验:从不等式组的解集中找出符合题意的答案;6、答:写出问题答案.
-
科目: 来源: 题型:
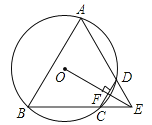
查看答案和解析>>【题目】如图,四边形ABCD是⊙O的内接四边形,BC的延长线与AD的延长线交于点E,且DC=DE.
(1)求证:∠A=∠AEB;
(2)连接OE,交CD于点F,OE⊥CD,求证:△ABE是等边三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在⊙O中,直径AB=6,BC是弦,∠ABC=30°,点P在BC上,点Q在⊙O上,且OP⊥PQ.
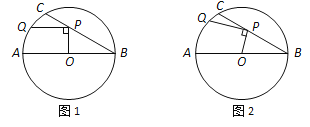
(1)如图1,当PQ∥AB时,求PQ的长度;
(2)如图2,当点P在BC上移动时,求PQ长的最大值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列成语或词组所描述的事件,不可能事件的是( )
A.守株待兔B.水中捞月C.瓮中捉鳖D.十拿九稳
-
科目: 来源: 题型:
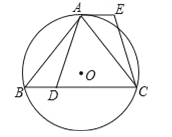
查看答案和解析>>【题目】已知:如图,⊙O是△ABC的外接圆,
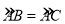 ,点D在边BC上,AE∥BC,AE=BD.
,点D在边BC上,AE∥BC,AE=BD.(1)求证:AD=CE;
(2)如果点G在线段DC上(不与点D重合),且AG=AD,求证:四边形AGCE是平行四边形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某村耕地总面积为50公顷,且该村人均耕地面积y(单位:公顷/人)与总人口x(单位:人)的函数图象如图所示,则下列说法正确的是( )
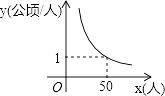
A.该村人均耕地面积随总人口的增多而增多
B.当该村总人口为50人时,人均耕地面积为1公顷
C.若该村人均耕地面积为2公顷,则总人口有100人
D.该村人均耕地面积y与总人口x成正比例 -
科目: 来源: 题型:
查看答案和解析>>【题目】计算(﹣2x2)3x的结果是( )
A.﹣6x6
B.8x6
C.﹣8x7
D.8x7
相关试题

